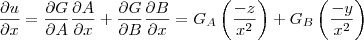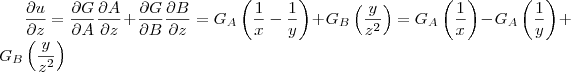por Jorge Dias » Sáb Jan 07, 2012 01:08
por Jorge Dias » Sáb Jan 07, 2012 01:08

mostre, que
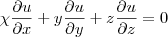
penso que tenho que achar as derivadas parciais,ou seja será que devo de achar o meu A como
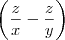
e o B, como

e apartir dai obter

mas não sei como fazer essa derivada e nem o que fazer com a icógnita que está antes da fracção
-
Jorge Dias
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Jan 06, 2012 23:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: licenciatura em gestão
- Andamento: cursando
 por ant_dii » Sáb Jan 07, 2012 02:29
por ant_dii » Sáb Jan 07, 2012 02:29
Jorge Dias escreveu:
mostre, que
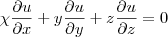
penso que tenho que achar as derivadas parciais,ou seja será que devo de achar o meu A como
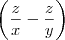
e o B, como

e apartir dai obter

mas não sei como fazer essa derivada e nem o que fazer com a icógnita que está antes da fracção
Se
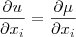
então você terá que usar a regra da cadeia, pois
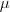
está em função de

por
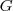
... E se

, então você terá que calcular cada derivada em função de uma incógnita de cada vez e depois multiplicar como esta pedindo acima e então procurar uma relação que de zero pra você mostrar o resultado desejado...
O que quero dizer é que do modo que esta escrito acima esta confuso... Quem são estes A, B e C que você fala e o

de

, é da onde?
O que pede na fórmula é só que você faça as derivadas (regra da cadeia) em relação a cada variável e depois verifique o resultado quando você multiplica a derivada com a variável.
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por Jorge Dias » Sáb Jan 07, 2012 10:36
por Jorge Dias » Sáb Jan 07, 2012 10:36
No livro tenho um exemplo que refere assim, sejam A e B as váriáveis mudas associadas á função G, ou seja U= G(A;B)= G

e então pela regra da cadeia temos
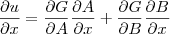
e assim sucessivamente para as outras icógnitas y e z é isso o que se pretende? mas não consigo iniciar estas derivadas.
-
Jorge Dias
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Jan 06, 2012 23:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: licenciatura em gestão
- Andamento: cursando
 por ant_dii » Sáb Jan 07, 2012 13:02
por ant_dii » Sáb Jan 07, 2012 13:02
Jorge Dias escreveu:No livro tenho um exemplo que refere assim, sejam A e B as váriáveis mudas associadas á função G, ou seja U= G(A;B)= G

e então pela regra da cadeia temos
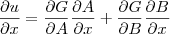
e assim sucessivamente para as outras icógnitas y e z é isso o que se pretende? mas não consigo iniciar estas derivadas.
Seguindo o que está em seu livro, temos que
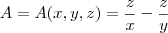

Então, mantenha

e faça

,
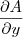
e
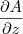
.
Mantenha
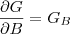
e faça
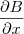
,

e
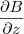
.
Por exemplo,
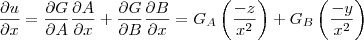
Em seguida, multiplique o resultado, como esta pedindo acima, por cada variável. Fazendo então uma manipulação algébrica você verá que o resultado será zero independente da derivada parcial de
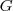
.
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por Jorge Dias » Sáb Jan 07, 2012 14:55
por Jorge Dias » Sáb Jan 07, 2012 14:55
pode me explicar porque não está fácil de entender para mim como fez a conta
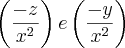
,não consigo chegar a esse valor
-
Jorge Dias
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Jan 06, 2012 23:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: licenciatura em gestão
- Andamento: cursando
 por ant_dii » Sáb Jan 07, 2012 15:19
por ant_dii » Sáb Jan 07, 2012 15:19
Sim... me desculpe.
A derivada de
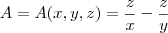
pode ser feita como segue, o mesmo valerá para as outras variáveis e para

:

Quando você deriva em relação a variável precedente as outras se tornam constantes, mas vale as mesmas regras para derivadas com uma variável...
Não sei se esclareceu, mas fique a vontade qualquer dúvida...
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por Jorge Dias » Sáb Jan 07, 2012 15:35
por Jorge Dias » Sáb Jan 07, 2012 15:35
muito obrigado pelo esclarecimento e sua disponibilidade.
-
Jorge Dias
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Jan 06, 2012 23:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: licenciatura em gestão
- Andamento: cursando
 por Jorge Dias » Sáb Jan 07, 2012 20:48
por Jorge Dias » Sáb Jan 07, 2012 20:48
muito obrigada pela ajuda, mas realmente não chego lá e não consigo fazer as contas de derivadas, estou a tentar mas ao calcular oa variável z empacou e não vai lá, e enquanto eu não conseguir fazer as derivadas bem não vou conseguir fazer este tipo de exercicios, percebo o que se pretende e não sei fazer as contas.
-
Jorge Dias
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Jan 06, 2012 23:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: licenciatura em gestão
- Andamento: cursando
 por ant_dii » Seg Jan 09, 2012 02:12
por ant_dii » Seg Jan 09, 2012 02:12
ant_dii escreveu:Sim... me desculpe.
A derivada de
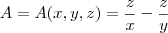
pode ser feita como segue, o mesmo valerá para as outras variáveis e para

:

Quando você deriva em relação a variável precedente as outras se tornam constantes, mas vale as mesmas regras para derivadas com uma variável...
Não sei se esclareceu, mas fique a vontade qualquer dúvida...
Vamos lá, que vou te ajudar então.
Para calcular a derivada de

em relação a

será usado o mesmo procedimento que foi em relação a

(como esta na citação acima), ou seja,

Para calcular

em relação a

, é feito o seguinte

De outra forma, pode-se fazer o seguinte

isso, pois como estamos derivando em relação a

, como já te disse, as outras variáveis se tornam constantes, então

e

também são constantes.
Em relação a

, você encontrará os seguintes resultados:
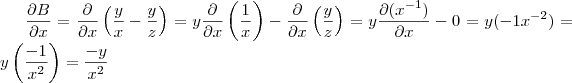
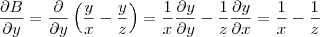
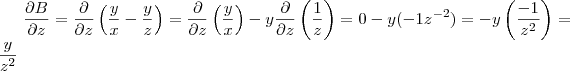
A partir daqui basta você fazer as derivadas de

em relação a cada variável usando os resultados já encontrados:
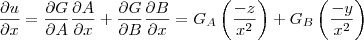

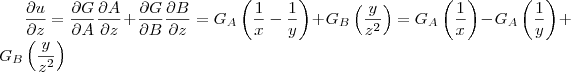
Agora entra a parte de manipulação. Quando você mexer certinho multiplicando pela variável precedente você obterá o resultado desejado...
Estamos ae qualquer coisa
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por Jorge Dias » Seg Jan 09, 2012 10:17
por Jorge Dias » Seg Jan 09, 2012 10:17
Muito agredecido pela ajuda prestada já cheguei ao resultado, tambem quase que me fez o exercicio todo, sua ajuda foi preciosa, consegui entender, é conta que nunca mais acaba.
-
Jorge Dias
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Jan 06, 2012 23:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: licenciatura em gestão
- Andamento: cursando
 por ant_dii » Ter Jan 10, 2012 00:16
por ant_dii » Ter Jan 10, 2012 00:16
Que nada... Foi bom te ajudar...
Quanto as contas, aprendi uma coisa: Matemática é 95% trabalho e 5% inteligência. Então existe muito trabalho a se fazer e muita pratica também ajudará...
Qualquer dúvida disponha...
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função diferencial
por baianinha » Qua Jun 29, 2011 22:43
- 3 Respostas
- 2258 Exibições
- Última mensagem por LuizAquino

Ter Jul 05, 2011 17:58
Cálculo: Limites, Derivadas e Integrais
-
- Diferencial de uma função com várias variáveis
por Fernandobertolaccini » Qui Dez 25, 2014 18:16
- 2 Respostas
- 2394 Exibições
- Última mensagem por Russman

Sáb Dez 27, 2014 00:21
Cálculo: Limites, Derivadas e Integrais
-
- Equação diferencial não-linear de função composta
 por Sally » Ter Fev 28, 2017 17:37
por Sally » Ter Fev 28, 2017 17:37
- 0 Respostas
- 2701 Exibições
- Última mensagem por Sally

Ter Fev 28, 2017 17:37
Cálculo: Limites, Derivadas e Integrais
-
- [Diferencial] Diferencial total
por temujin » Qua Mai 29, 2013 17:10
- 2 Respostas
- 1258 Exibições
- Última mensagem por temujin

Ter Out 21, 2014 17:17
Cálculo: Limites, Derivadas e Integrais
-
- Equação Diferencial.
por Higor » Seg Fev 21, 2011 13:12
- 4 Respostas
- 12215 Exibições
- Última mensagem por Higor

Seg Fev 21, 2011 14:46
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

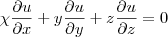
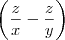 e o B, como
e o B, como  e apartir dai obter
e apartir dai obter  mas não sei como fazer essa derivada e nem o que fazer com a icógnita que está antes da fracção
mas não sei como fazer essa derivada e nem o que fazer com a icógnita que está antes da fracção

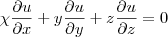
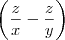 e o B, como
e o B, como  e apartir dai obter
e apartir dai obter  mas não sei como fazer essa derivada e nem o que fazer com a icógnita que está antes da fracção
mas não sei como fazer essa derivada e nem o que fazer com a icógnita que está antes da fracção
e o B, como
e apartir dai obter
mas não sei como fazer essa derivada e nem o que fazer com a icógnita que está antes da fracção
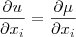
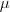 está em função de
está em função de  por
por 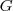 ... E se
... E se  , então você terá que calcular cada derivada em função de uma incógnita de cada vez e depois multiplicar como esta pedindo acima e então procurar uma relação que de zero pra você mostrar o resultado desejado...
, então você terá que calcular cada derivada em função de uma incógnita de cada vez e depois multiplicar como esta pedindo acima e então procurar uma relação que de zero pra você mostrar o resultado desejado... de
de  , é da onde?
, é da onde?
 e então pela regra da cadeia temos
e então pela regra da cadeia temos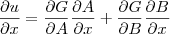

e então pela regra da cadeia temos
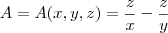

 e faça
e faça  ,
, 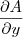 e
e 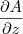 .
.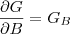 e faça
e faça 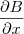 ,
,  e
e 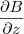 .
.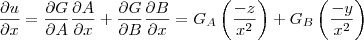
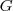 .
.
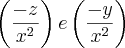 ,não consigo chegar a esse valor
,não consigo chegar a esse valor
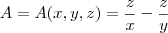 pode ser feita como segue, o mesmo valerá para as outras variáveis e para
pode ser feita como segue, o mesmo valerá para as outras variáveis e para  :
:



pode ser feita como segue, o mesmo valerá para as outras variáveis e para
:
 em relação a
em relação a  será usado o mesmo procedimento que foi em relação a
será usado o mesmo procedimento que foi em relação a  (como esta na citação acima), ou seja,
(como esta na citação acima), ou seja,
 em relação a
em relação a  , é feito o seguinte
, é feito o seguinte

 , como já te disse, as outras variáveis se tornam constantes, então
, como já te disse, as outras variáveis se tornam constantes, então  e
e  também são constantes.
também são constantes. , você encontrará os seguintes resultados:
, você encontrará os seguintes resultados: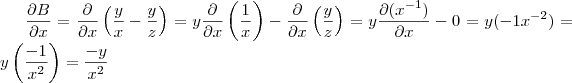
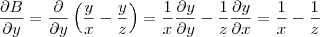
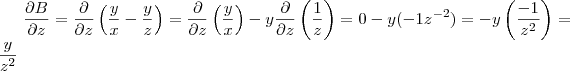
 em relação a cada variável usando os resultados já encontrados:
em relação a cada variável usando os resultados já encontrados: