 por VFernandes » Ter Jan 03, 2012 23:47
por VFernandes » Ter Jan 03, 2012 23:47
Caros amigos,
Estou enfrentando um problema de integração, onde tenho que calcular uma integral definida através de um método numérico chamado de Método de Romberg. Tudo é bem mecânico quando a função é bem comportada no intervalo de integração, mas quando me deparo com o exemplo:
![\int_0^{\pi/2} \sqrt[]{x}*cos(x) dx \int_0^{\pi/2} \sqrt[]{x}*cos(x) dx](/latexrender/pictures/9f9b4555ac537d96e98c123fac1c6805.png)
não consigo integrar pois a derivada da função no ponto 0 tende ao infinito. Nesse caso, tenho que usar um macete, e fazer a mudança de variável
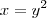
. Dessa forma, a integral fica regularizada e o método funciona.
Agora vem a zica. Dada a integral:
![\int_0^1 \frac{cos(x)}{\sqrt[]{x(1-x)}} dx \int_0^1 \frac{cos(x)}{\sqrt[]{x(1-x)}} dx](/latexrender/pictures/0591327d52246a8d4ccf1e6579e8c669.png)
Eu não consigo achar, de jeito nenhum, uma mudança de variável que regularize a função e me permita fazer a integração numérica.
Alguém tem uma luz? Já tentei
![x = y^2, x = \sqrt[]{y}, x = sen(y) x = y^2, x = \sqrt[]{y}, x = sen(y)](/latexrender/pictures/832f4c4d74b2c561c2f874a446b97944.png)
e nada funcionou...
Profundamente agradecido,
-
VFernandes
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sex Mar 04, 2011 16:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Elétrica
- Andamento: cursando
 por fraol » Qui Jan 05, 2012 08:53
por fraol » Qui Jan 05, 2012 08:53
Bom dia,
Também tentei algumas alternativas de substituição sem sucesso. Usando integração por partes caímos numa recorrência. Pesquisando na net achei esse post
http://www.artofproblemsolving.com/Forum/viewtopic.php?f=296&t=452952 que trata a solução via a equação de Bessel. Isto é faz-se uma substituição conveniente de forma a recair numa equação de Bessel.
Outra maneira de resolver seria transformar a função dada numa série de Taylor em torno de 0 por exemplo, pegar um número pequeno de termos e então calcular a integral o que vai dar uma boa aproximação.
Vou estudar o Método de Romberg.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por VFernandes » Qui Jan 05, 2012 23:32
por VFernandes » Qui Jan 05, 2012 23:32
Caros amigos, problema resolvido!
Vejam esse artigo (em especial o terceiro capítulo):
http://faculty.smu.edu/shampine/MA5315/SingQuad.pdfEncontrei duas soluções para o problema:
1)
Se dividirmos a integral em duas, uma de 0 a 0.5 e outra de 0.5 a 1, poderemos trabalhar com uma singularidade de cada vez e aí basta fazermos:
(1ª integral)
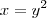
e a função fica
![f(y) = 2*\frac{cos(y^2)}{\sqrt[]{1-y^2}} f(y) = 2*\frac{cos(y^2)}{\sqrt[]{1-y^2}}](/latexrender/pictures/5b6bcec8526b7b707d40fe45cd738161.png)
que é regular no intervalo de integração desejado (
![[0,\sqrt[]{1/2}] [0,\sqrt[]{1/2}]](/latexrender/pictures/4f37173a4a019c0cae5c1369aa85d8c9.png)
).
(2ª integral)

e a função fica
![f(y) = 2*\frac{cos(1-y^2)}{\sqrt[]{1-y^2}} f(y) = 2*\frac{cos(1-y^2)}{\sqrt[]{1-y^2}}](/latexrender/pictures/4e61a611f01eecc40bfa0a83729313f0.png)
que também é regular no intervalo desejado (
![[0,\sqrt[]{1/2}] [0,\sqrt[]{1/2}]](/latexrender/pictures/4f37173a4a019c0cae5c1369aa85d8c9.png)
).
2)
Essa é ainda mais fácil.
Se fizermos a substituição
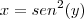
, a função ficará da forma

que é perfeitamente regular e facilmente integravel no intervalo
![[0,\pi/2] [0,\pi/2]](/latexrender/pictures/6b59bc315c28725e04e9331e71527914.png)
.
Abraços,
-
VFernandes
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sex Mar 04, 2011 16:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Mudança de variavel na integral
por matmatco » Ter Abr 23, 2013 22:29
- 0 Respostas
- 1119 Exibições
- Última mensagem por matmatco

Ter Abr 23, 2013 22:29
Cálculo: Limites, Derivadas e Integrais
-
- [Integral Dupla] Imagem do conjunto S - Mudança de Variável
por neymeirelles » Qua Mai 23, 2012 21:14
- 2 Respostas
- 2681 Exibições
- Última mensagem por neymeirelles

Sex Mai 25, 2012 12:18
Cálculo: Limites, Derivadas e Integrais
-
- [Integral Dupla] Com mudança de Variável - Está certo?
por RafaelOx » Sex Jun 21, 2013 00:36
- 1 Respostas
- 2487 Exibições
- Última mensagem por young_jedi

Sex Jun 21, 2013 21:04
Cálculo: Limites, Derivadas e Integrais
-
- Mudança de Variável
por DanielFerreira » Dom Abr 22, 2012 13:58
- 2 Respostas
- 1603 Exibições
- Última mensagem por DanielFerreira

Ter Abr 24, 2012 20:31
Cálculo: Limites, Derivadas e Integrais
-
- Mudança de Variável
 por DanielFerreira » Dom Abr 29, 2012 21:06
por DanielFerreira » Dom Abr 29, 2012 21:06
- 3 Respostas
- 1870 Exibições
- Última mensagem por LuizAquino

Ter Mai 01, 2012 15:56
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_0^{\pi/2} \sqrt[]{x}*cos(x) dx \int_0^{\pi/2} \sqrt[]{x}*cos(x) dx](/latexrender/pictures/9f9b4555ac537d96e98c123fac1c6805.png)
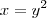 . Dessa forma, a integral fica regularizada e o método funciona.
. Dessa forma, a integral fica regularizada e o método funciona.![\int_0^1 \frac{cos(x)}{\sqrt[]{x(1-x)}} dx \int_0^1 \frac{cos(x)}{\sqrt[]{x(1-x)}} dx](/latexrender/pictures/0591327d52246a8d4ccf1e6579e8c669.png)
![x = y^2, x = \sqrt[]{y}, x = sen(y) x = y^2, x = \sqrt[]{y}, x = sen(y)](/latexrender/pictures/832f4c4d74b2c561c2f874a446b97944.png) e nada funcionou...
e nada funcionou...


![f(y) = 2*\frac{cos(y^2)}{\sqrt[]{1-y^2}} f(y) = 2*\frac{cos(y^2)}{\sqrt[]{1-y^2}}](/latexrender/pictures/5b6bcec8526b7b707d40fe45cd738161.png) que é regular no intervalo de integração desejado (
que é regular no intervalo de integração desejado (![[0,\sqrt[]{1/2}] [0,\sqrt[]{1/2}]](/latexrender/pictures/4f37173a4a019c0cae5c1369aa85d8c9.png) ).
). e a função fica
e a função fica ![f(y) = 2*\frac{cos(1-y^2)}{\sqrt[]{1-y^2}} f(y) = 2*\frac{cos(1-y^2)}{\sqrt[]{1-y^2}}](/latexrender/pictures/4e61a611f01eecc40bfa0a83729313f0.png) que também é regular no intervalo desejado (
que também é regular no intervalo desejado (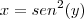 , a função ficará da forma
, a função ficará da forma  que é perfeitamente regular e facilmente integravel no intervalo
que é perfeitamente regular e facilmente integravel no intervalo ![[0,\pi/2] [0,\pi/2]](/latexrender/pictures/6b59bc315c28725e04e9331e71527914.png) .
.

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.