[Cálculo Integral] Mudança de variável

por **VFernandes** » Ter Jan 03, 2012 23:47

Caros amigos,

Estou enfrentando um problema de integração, onde tenho que calcular uma integral definida através de um método numérico chamado de Método de Romberg. Tudo é bem mecânico quando a função é bem comportada no intervalo de integração, mas quando me deparo com o exemplo:

$\int_0^{\pi/2} \sqrt[]{x}*cos(x) dx$

não consigo integrar pois a derivada da função no ponto 0 tende ao infinito. Nesse caso, tenho que usar um macete, e fazer a mudança de variável x = y^2

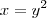. Dessa forma, a integral fica regularizada e o método funciona.

Agora vem a zica. Dada a integral:

$\int_0^1 \frac{cos(x)}{\sqrt[]{x(1-x)}} dx$

Eu não consigo achar, de jeito nenhum, uma mudança de variável que regularize a função e me permita fazer a integração numérica.

Alguém tem uma luz? Já tentei $x = y^2, x = \sqrt[]{y}, x = sen(y)$ e nada funcionou...

Profundamente agradecido,

por **fraol** » Qui Jan 05, 2012 08:53

Bom dia,

Também tentei algumas alternativas de substituição sem sucesso. Usando integração por partes caímos numa recorrência. Pesquisando na net achei esse post http://www.artofproblemsolving.com/Forum/viewtopic.php?f=296&t=452952 que trata a solução via a equação de Bessel. Isto é faz-se uma substituição conveniente de forma a recair numa equação de Bessel.
Outra maneira de resolver seria transformar a função dada numa série de Taylor em torno de 0 por exemplo, pegar um número pequeno de termos e então calcular a integral o que vai dar uma boa aproximação.

Vou estudar o Método de Romberg.

por **VFernandes** » Qui Jan 05, 2012 23:32

Caros amigos, problema resolvido!
Vejam esse artigo (em especial o terceiro capítulo): http://faculty.smu.edu/shampine/MA5315/SingQuad.pdf
Encontrei duas soluções para o problema:

1)
Se dividirmos a integral em duas, uma de 0 a 0.5 e outra de 0.5 a 1, poderemos trabalhar com uma singularidade de cada vez e aí basta fazermos:
(1ª integral) x = y^2

e a função fica $f(y) = 2*\frac{cos(y^2)}{\sqrt[]{1-y^2}}$ que é regular no intervalo de integração desejado ( $[0,\sqrt[]{1/2}]$ ).
(2ª integral) x = y^2 + 1

e a função fica $f(y) = 2*\frac{cos(1-y^2)}{\sqrt[]{1-y^2}}$ que também é regular no intervalo desejado ( $[0,\sqrt[]{1/2}]$ ).

2)
Essa é ainda mais fácil.
Se fizermos a substituição x = sen^2(y)

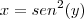, a função ficará da forma f(y) = 2cos(sen(y))

que é perfeitamente regular e facilmente integravel no intervalo $[0,\pi/2]$ .

Abraços,

[Cálculo Integral] Mudança de variável

[Cálculo Integral] Mudança de variável

[Cálculo Integral] Mudança de variável

Re: [Cálculo Integral] Mudança de variável

Re: [Cálculo Integral] Mudança de variável

Quem está online