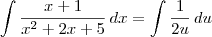por Marcio Cristo » Qui Dez 22, 2011 18:35
por Marcio Cristo » Qui Dez 22, 2011 18:35
Boa tarde , como ficaria a seguinte integral? A minha duvida é por onde começar e como ficaria a fatoração do polinomio que está no denominador . Se puder fazer um passo a passo . Agradeço desde ja .
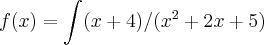
-
Marcio Cristo
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Dez 22, 2011 18:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por LuizAquino » Qui Dez 22, 2011 22:01
por LuizAquino » Qui Dez 22, 2011 22:01
Marcio Cristo escreveu:Boa tarde , como ficaria a seguinte integral? A minha duvida é por onde começar e como ficaria a fatoração do polinomio que está no denominador . Se puder fazer um passo a passo . Agradeço desde ja.
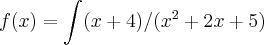
Para estudar a resolução dessa integral, siga o procedimento abaixo.
- Acesse a página: http://www.wolframalpha.com/
- No campo de entrada, digite:
- Código: Selecionar todos
integrate (x+4)/(x^2+2x+5) dx
- Clique no botão de igual ao lado do campo de entrada.
- Após a integral ser calculada, clique no botão "Show steps" ao lado do resultado.
- Pronto! Agora basta estudar a resolução e comparar com a sua.
ObservaçãoSe você desejar revisar as técnicas de integração, então eu gostaria de recomendar que você assista as vídeo-aulas disponíveis em meu canal no YouTube:
http://www.youtube.com/LCMAquino
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Marcio Cristo » Qui Dez 22, 2011 22:23
por Marcio Cristo » Qui Dez 22, 2011 22:23
Boa noite, obrigado pelo feeedback , Luiz , noto que x+4/x^2+2x+5 foi reescrito na forma de 2x+2 / 2( x^2+2x+5) + 3/x^2+2x+5 , qual a tecnica usada para essa transformação de polinomios ??? como ele chegou a tal ???
-
Marcio Cristo
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Dez 22, 2011 18:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por Marcio Cristo » Sex Dez 23, 2011 17:36
por Marcio Cristo » Sex Dez 23, 2011 17:36
entendi , agora , qual a finalidade de ter multiplicado a primeira expressão toda por 2 ?? não poderia integrar com aquele polinomio x+1 ??
-
Marcio Cristo
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Dez 22, 2011 18:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por LuizAquino » Sex Dez 23, 2011 18:00
por LuizAquino » Sex Dez 23, 2011 18:00
Marcio Cristo escreveu:qual a finalidade de ter multiplicado a primeira expressão toda por 2 ?? não poderia integrar com aquele polinomio x+1 ??
A finalidade foi de "facilitar" o uso da integração por substituição.
Note que fazendo

e
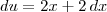
, temos que :
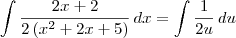
Obviamente, também poderíamos utilizar essa mesma substituição sem usar esse artifício de multiplicar a priori por 2.
Note que podemos reescrever
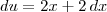
como sendo
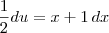
. Nesse caso, podemos escrever diretamente que:
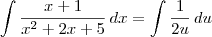
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Técnicas de integração
por Victor Mello » Seg Nov 18, 2013 23:04
- 2 Respostas
- 1646 Exibições
- Última mensagem por Victor Mello

Ter Nov 19, 2013 00:16
Cálculo: Limites, Derivadas e Integrais
-
- [tecnicas de integraçao por partes (u)(dv)]
por menino de ouro » Ter Out 30, 2012 18:21
- 3 Respostas
- 2079 Exibições
- Última mensagem por MarceloFantini

Ter Out 30, 2012 22:39
Cálculo: Limites, Derivadas e Integrais
-
- [Tecnicas de integraçao por substiuiçao simples]
por menino de ouro » Qua Out 24, 2012 16:12
- 1 Respostas
- 1502 Exibições
- Última mensagem por young_jedi

Qua Out 24, 2012 16:51
Cálculo: Limites, Derivadas e Integrais
-
- Técnicas de integração - multiplicando pelo fator unitário
por Victor Mello » Qui Nov 21, 2013 18:37
- 2 Respostas
- 1709 Exibições
- Última mensagem por Victor Mello

Qui Nov 21, 2013 23:27
Cálculo: Limites, Derivadas e Integrais
-
- [ Inequaçoes Quadráticas-Técnicas]
por R0nny » Qua Mai 01, 2013 17:02
- 0 Respostas
- 1059 Exibições
- Última mensagem por R0nny

Qua Mai 01, 2013 17:02
Inequações
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
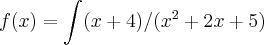


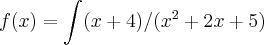



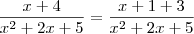
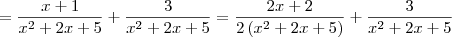


 e
e 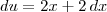 , temos que :
, temos que :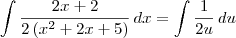
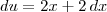 como sendo
como sendo 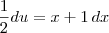 . Nesse caso, podemos escrever diretamente que:
. Nesse caso, podemos escrever diretamente que: