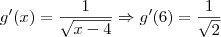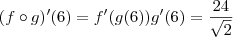por Saruka » Sex Nov 11, 2011 18:26
por Saruka » Sex Nov 11, 2011 18:26
Estou com alguma pressa em saber a resolução de um exercicio que saiu numa frequencia de analise do ano passado na universidade que frequento.
Calcule, usando o Teorema da derivada da funçao composta (fog)' (6)
![f(x)={x}^{3} +1\;\;\;\;\;\;g(x)= 2\sqrt[2]{x-4} f(x)={x}^{3} +1\;\;\;\;\;\;g(x)= 2\sqrt[2]{x-4}](/latexrender/pictures/d79f2de1fe75e7d62f895e6ab8f5169b.png)
O que fiz foi:
![3({2\sqrt[2]{x-4}}^{2}) = 3 [4(x-4)] = 12x-48 3({2\sqrt[2]{x-4}}^{2}) = 3 [4(x-4)] = 12x-48](/latexrender/pictures/57190f7efe8d4840192773cc70871568.png)
Chegando à parte em que tenho que fazer a derivada de g empanquei mesmo. Fiz:
![[2(\frac{1}{2} * {x-4}^{\frac{-1}{2}} * (x-4)'\:] [2(\frac{1}{2} * {x-4}^{\frac{-1}{2}} * (x-4)'\:]](/latexrender/pictures/a6f26d6ad68875e8b4c9b7a27e51fc62.png)
Alguem me pode ajudar a entender como se faz a derivada com raiz?
-
Saruka
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Nov 11, 2011 18:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em engenharia informatica
- Andamento: cursando
 por Saruka » Sex Nov 11, 2011 18:33
por Saruka » Sex Nov 11, 2011 18:33
Na parte do
![3({2\sqrt[2]{x-4}}^{2}) = 3 [4(x-4)] = 12x-48 3({2\sqrt[2]{x-4}}^{2}) = 3 [4(x-4)] = 12x-48](/latexrender/pictures/57190f7efe8d4840192773cc70871568.png)
o está tudo elevado ao quadrado excepto o 3
-
Saruka
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Nov 11, 2011 18:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em engenharia informatica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Duvida] Derivada da Composta
por demolot » Qua Mai 25, 2011 13:04
- 4 Respostas
- 2076 Exibições
- Última mensagem por demolot

Qui Mai 26, 2011 12:55
Cálculo: Limites, Derivadas e Integrais
-
- Derivada - função composta
por core » Qua Out 16, 2013 15:54
- 1 Respostas
- 1330 Exibições
- Última mensagem por Taka

Sáb Nov 02, 2013 21:12
Cálculo: Limites, Derivadas e Integrais
-
- Derivada de função composta
por Fernandobertolaccini » Qua Jul 09, 2014 08:37
- 0 Respostas
- 911 Exibições
- Última mensagem por Fernandobertolaccini

Qua Jul 09, 2014 08:37
Cálculo: Limites, Derivadas e Integrais
-
- derivada de função composta.
por nandooliver008 » Dom Set 21, 2014 19:42
- 1 Respostas
- 1227 Exibições
- Última mensagem por Cleyson007

Seg Set 22, 2014 18:04
Cálculo: Limites, Derivadas e Integrais
-
- Problema com a derivada de uma função composta
por DavidUserCalc » Qui Abr 01, 2010 14:44
- 1 Respostas
- 1952 Exibições
- Última mensagem por Molina

Qui Abr 01, 2010 16:56
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![f(x)={x}^{3} +1\;\;\;\;\;\;g(x)= 2\sqrt[2]{x-4} f(x)={x}^{3} +1\;\;\;\;\;\;g(x)= 2\sqrt[2]{x-4}](/latexrender/pictures/d79f2de1fe75e7d62f895e6ab8f5169b.png)
![3({2\sqrt[2]{x-4}}^{2}) = 3 [4(x-4)] = 12x-48 3({2\sqrt[2]{x-4}}^{2}) = 3 [4(x-4)] = 12x-48](/latexrender/pictures/57190f7efe8d4840192773cc70871568.png)
![[2(\frac{1}{2} * {x-4}^{\frac{-1}{2}} * (x-4)'\:] [2(\frac{1}{2} * {x-4}^{\frac{-1}{2}} * (x-4)'\:]](/latexrender/pictures/a6f26d6ad68875e8b4c9b7a27e51fc62.png)

![f(x)={x}^{3} +1\;\;\;\;\;\;g(x)= 2\sqrt[2]{x-4} f(x)={x}^{3} +1\;\;\;\;\;\;g(x)= 2\sqrt[2]{x-4}](/latexrender/pictures/d79f2de1fe75e7d62f895e6ab8f5169b.png)
![3({2\sqrt[2]{x-4}}^{2}) = 3 [4(x-4)] = 12x-48 3({2\sqrt[2]{x-4}}^{2}) = 3 [4(x-4)] = 12x-48](/latexrender/pictures/57190f7efe8d4840192773cc70871568.png)
![[2(\frac{1}{2} * {x-4}^{\frac{-1}{2}} * (x-4)'\:] [2(\frac{1}{2} * {x-4}^{\frac{-1}{2}} * (x-4)'\:]](/latexrender/pictures/a6f26d6ad68875e8b4c9b7a27e51fc62.png)

![3({2\sqrt[2]{x-4}}^{2}) = 3 [4(x-4)] = 12x-48 3({2\sqrt[2]{x-4}}^{2}) = 3 [4(x-4)] = 12x-48](/latexrender/pictures/57190f7efe8d4840192773cc70871568.png)

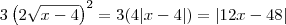
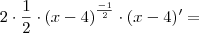
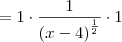
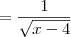
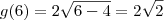
![f^\prime (x)=3x^2 \Rightarrow f^\prime (g(6)) = 3[g(6)]^2 \Rightarrow f^\prime \left(2\sqrt{2}\right) = 24 f^\prime (x)=3x^2 \Rightarrow f^\prime (g(6)) = 3[g(6)]^2 \Rightarrow f^\prime \left(2\sqrt{2}\right) = 24](/latexrender/pictures/0ba993614b0ac4e141763827e489f6e6.png)