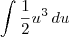por ah001334 » Seg Out 17, 2011 13:08
por ah001334 » Seg Out 17, 2011 13:08
Olá Pessoal,
Estou com uma dúvida em uma integral sendo que
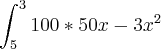
separei elas, coloquei o 100 para fora da integral, pois é um número inteiro e os demais separei em duas integrais uma 50x e a outra -3x elevada na 2 encontrei o resultado 100*25x elevado na 2 - x elevado na 3 mas o resultado nao fecha com o da profe que é 888? o que tenho feito de errado?
-
ah001334
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Seg Out 17, 2011 12:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por LuizAquino » Seg Out 17, 2011 13:47
por LuizAquino » Seg Out 17, 2011 13:47
A integral que você deseja resolver é esta:
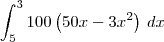
?
O que você escreveu foi
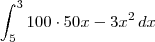
, que seria o mesmo que
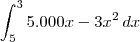
.
Se a integral que você deseja é a primeira que eu escrevi, então basta fazer:


![= 100\left[25x^2\right]_5^3 - 100 \left[x^3\right]_5^3 = 100\left[25x^2\right]_5^3 - 100 \left[x^3\right]_5^3](/latexrender/pictures/567f9433038e00754bad75f5881166af.png)
 Observação
ObservaçãoEu recomendo que você leia o tópico:
DICA: Escrevendo Fórmulas com LaTeX via BBCodeviewtopic.php?f=9&t=74Se precisar, use também o
Editor de Fórmulas.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por ah001334 » Seg Out 17, 2011 14:27
por ah001334 » Seg Out 17, 2011 14:27
A questão seria: Suponha que a função seja

quando o nível de produção é x. Encontre o valor do lucro obtido com a venda de 3 unidades adicionais, se atualmente 5 unidades estão sendo produzidas.
Essa é questão, por isso me refiro que os limites serão 3 e 5 e separei a integral com adição e subtração mas nao fecha o resultado o meu resultado foi

-
ah001334
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Seg Out 17, 2011 12:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por LuizAquino » Seg Out 17, 2011 15:26
por LuizAquino » Seg Out 17, 2011 15:26
ah001334 escreveu:A questão seria: Suponha que a função seja

quando o nível de produção é x. Encontre o valor do lucro obtido com a venda de 3 unidades adicionais, se atualmente 5 unidades estão sendo produzidas.
Isto já está bem diferente do que você enviou da primeira vez!

Além disso, ainda parece faltar informações nesse enunciado. Não haveria algum texto antes desse? Por exemplo, o que representa a função
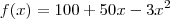
? Isso não está informado nesse enunciado! Por acaso estaria relacionada com o lucro?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por ah001334 » Seg Out 17, 2011 15:44
por ah001334 » Seg Out 17, 2011 15:44
sim está relacionada ao lucro
Veja o desenvolvimento da integral
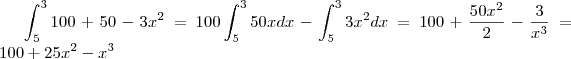
-
ah001334
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Seg Out 17, 2011 12:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por LuizAquino » Seg Out 17, 2011 17:11
por LuizAquino » Seg Out 17, 2011 17:11
ah001334 escreveu:Veja o desenvolvimento da integral

Isso está errado.
A solução correta seria como segue.
Já que o nível estava em 5 unidades e foram adicionadas 3 unidades, então você passou para um nível de 8 unidades.
Você deve então resolver:

![= \left[100x\right]_5^8 + \left[25x^2\right]_5^8 - \left[x^3\right]_5^8 = \left[100x\right]_5^8 + \left[25x^2\right]_5^8 - \left[x^3\right]_5^8](/latexrender/pictures/1c5ab4eb0b0804b6ced446b78fea4e56.png)
 Observação
ObservaçãoUma solução mais curta é apenas fazer:
![\int_{5}^{8} 100+50x-3{x}^{2} \,dx = \left[100x +25x^2 - x^3\right]_5^8 \int_{5}^{8} 100+50x-3{x}^{2} \,dx = \left[100x +25x^2 - x^3\right]_5^8](/latexrender/pictures/694e8c5445c0f17a8737b549a964097c.png)
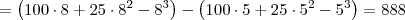
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por ah001334 » Ter Out 18, 2011 13:12
por ah001334 » Ter Out 18, 2011 13:12
Muito obrigada!!!
-
ah001334
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Seg Out 17, 2011 12:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por ah001334 » Ter Out 18, 2011 13:53
por ah001334 » Ter Out 18, 2011 13:53
Mais uma dúvida veja a integral abaixo:
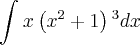
estou resolvendo por substituição como segue abaixo:

[tex]u={x}^{2}+1
[tex]\int_{}^{}x\left(u \right){}^{3}* \frac{du}{2x}
o que faço com o 3 que está elevando o u?
-
ah001334
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Seg Out 17, 2011 12:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por LuizAquino » Ter Out 18, 2011 16:15
por LuizAquino » Ter Out 18, 2011 16:15
Você deseja resolver a integral

Fazendo a substituição
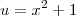
e

, essa integral por ser reescrita como
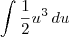
Agora tente terminar o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Resolver Integral definida com trigonometria
por rodrigoboreli » Dom Set 07, 2014 01:02
- 1 Respostas
- 4347 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo Integral] Integral Definida
por ARCS » Sáb Fev 02, 2013 21:37
- 2 Respostas
- 3684 Exibições
- Última mensagem por e8group

Sáb Fev 02, 2013 22:13
Cálculo: Limites, Derivadas e Integrais
-
- [integral] integral definida por partes
por gabriel feron » Seg Mar 11, 2013 00:48
- 2 Respostas
- 3075 Exibições
- Última mensagem por gabriel feron

Seg Mar 11, 2013 18:19
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Derivar integral definida
por troziinho » Ter Mar 31, 2015 20:26
- 0 Respostas
- 2500 Exibições
- Última mensagem por troziinho

Ter Mar 31, 2015 20:26
Cálculo: Limites, Derivadas e Integrais
-
- Integral definida
por exploit » Ter Set 07, 2010 19:17
- 4 Respostas
- 3627 Exibições
- Última mensagem por exploit

Qua Set 08, 2010 19:58
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
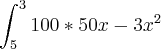 separei elas, coloquei o 100 para fora da integral, pois é um número inteiro e os demais separei em duas integrais uma 50x e a outra -3x elevada na 2 encontrei o resultado 100*25x elevado na 2 - x elevado na 3 mas o resultado nao fecha com o da profe que é 888? o que tenho feito de errado?
separei elas, coloquei o 100 para fora da integral, pois é um número inteiro e os demais separei em duas integrais uma 50x e a outra -3x elevada na 2 encontrei o resultado 100*25x elevado na 2 - x elevado na 3 mas o resultado nao fecha com o da profe que é 888? o que tenho feito de errado?

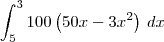 ?
?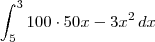 , que seria o mesmo que
, que seria o mesmo que 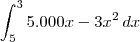 .
.

![= 100\left[25x^2\right]_5^3 - 100 \left[x^3\right]_5^3 = 100\left[25x^2\right]_5^3 - 100 \left[x^3\right]_5^3](/latexrender/pictures/567f9433038e00754bad75f5881166af.png)


 quando o nível de produção é x. Encontre o valor do lucro obtido com a venda de 3 unidades adicionais, se atualmente 5 unidades estão sendo produzidas.
quando o nível de produção é x. Encontre o valor do lucro obtido com a venda de 3 unidades adicionais, se atualmente 5 unidades estão sendo produzidas.

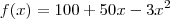 ? Isso não está informado nesse enunciado! Por acaso estaria relacionada com o lucro?
? Isso não está informado nesse enunciado! Por acaso estaria relacionada com o lucro?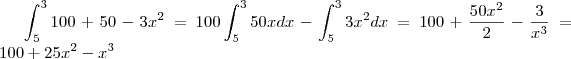


![= \left[100x\right]_5^8 + \left[25x^2\right]_5^8 - \left[x^3\right]_5^8 = \left[100x\right]_5^8 + \left[25x^2\right]_5^8 - \left[x^3\right]_5^8](/latexrender/pictures/1c5ab4eb0b0804b6ced446b78fea4e56.png)

![\int_{5}^{8} 100+50x-3{x}^{2} \,dx = \left[100x +25x^2 - x^3\right]_5^8 \int_{5}^{8} 100+50x-3{x}^{2} \,dx = \left[100x +25x^2 - x^3\right]_5^8](/latexrender/pictures/694e8c5445c0f17a8737b549a964097c.png)
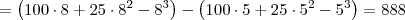
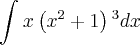 estou resolvendo por substituição como segue abaixo:
estou resolvendo por substituição como segue abaixo: [tex]u={x}^{2}+1
[tex]u={x}^{2}+1
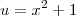 e
e  , essa integral por ser reescrita como
, essa integral por ser reescrita como