![\lim_{x\rightarrow1}\frac{\sqrt[5]{x}-\sqrt[3]{x}}{x-1} \lim_{x\rightarrow1}\frac{\sqrt[5]{x}-\sqrt[3]{x}}{x-1}](/latexrender/pictures/00a53dd977ca00c549bb7b8dbe5fab6b.png) a minha duvida é de como eu faço ao conjugado disso. sem usar derivada pois eu aindo vou aprender isso
a minha duvida é de como eu faço ao conjugado disso. sem usar derivada pois eu aindo vou aprender isso  .
.
![\lim_{x\rightarrow1}\frac{\sqrt[5]{x}-\sqrt[3]{x}}{x-1} \lim_{x\rightarrow1}\frac{\sqrt[5]{x}-\sqrt[3]{x}}{x-1}](/latexrender/pictures/00a53dd977ca00c549bb7b8dbe5fab6b.png) a minha duvida é de como eu faço ao conjugado disso. sem usar derivada pois eu aindo vou aprender isso
a minha duvida é de como eu faço ao conjugado disso. sem usar derivada pois eu aindo vou aprender isso  .
.
![\lim_{x\rightarrow{1}}\frac{\sqrt[3]{x}-\sqrt[3]{x}}{x-1} \lim_{x\rightarrow{1}}\frac{\sqrt[3]{x}-\sqrt[3]{x}}{x-1}](/latexrender/pictures/d7874cbfc35959bb33386639997b65db.png)






moyses escreveu:Bom pessoal tenho uma duvida nesse limite aqui:
 . Com isso, quando x tende para 1, temos que u também tende para 1. Além disso, podemos escrever que:
. Com isso, quando x tende para 1, temos que u também tende para 1. Além disso, podemos escrever que:![\lim_{x\to 1}\frac{\sqrt[5]{x}-\sqrt[3]{x}}{x-1} = \lim_{u\to 1}\frac{u^3 - u^5}{u^{15}-1} = \lim_{u\to 1}\frac{u^3\left(1 - u^2\right)}{u^{15}-1} \lim_{x\to 1}\frac{\sqrt[5]{x}-\sqrt[3]{x}}{x-1} = \lim_{u\to 1}\frac{u^3 - u^5}{u^{15}-1} = \lim_{u\to 1}\frac{u^3\left(1 - u^2\right)}{u^{15}-1}](/latexrender/pictures/91ad548d3af122966e5b38ab3399694f.png)


 , pois seria divisível por 3 e 5.
, pois seria divisível por 3 e 5.![\sqrt[5]{u^{15}}\Rightarrow u^\frac{15}{5}= u^3 \sqrt[5]{u^{15}}\Rightarrow u^\frac{15}{5}= u^3](/latexrender/pictures/162aeda40d0a3311ed9cde7b0affcc09.png)
![\sqrt[3]{u^{15}}\Rightarrow u^\frac{15}{3}= u^5 \sqrt[3]{u^{15}}\Rightarrow u^\frac{15}{3}= u^5](/latexrender/pictures/12cea3cbb416a435cbe3561b9ac06d01.png)

moyses escreveu:como assim não entendi o que você fez exatamente?
 foi realizada para simplificar os radicais existentes.
foi realizada para simplificar os radicais existentes.Claudin escreveu:Ele atribuiu, pois seria divisível por 3 e 5.
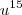 é divisível por 3 e 5, o que não faz sentido nesse contexto.
é divisível por 3 e 5, o que não faz sentido nesse contexto.

 !
! 

moyses escreveu:(...) por que embaixo você colocou x igual a u , sendo que x que você falou era u elevado a 15?
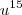 no denominador.
no denominador. . Se você não se recorda como efetuar a divisão entre polinômios, eu recomendo que você assista as vídeo-aulas:
. Se você não se recorda como efetuar a divisão entre polinômios, eu recomendo que você assista as vídeo-aulas:Claudin escreveu:Obs: Quando eu fui Colaborador oficial do fórum, tinha como ideal sempre nas discussões da sala fechada o detalhamento das questões, pois no meu entendimento a matemática se aprende praticando, e as vezes a pessoa martela, martela em exercício e não sai nada, talvez a saída seja estudar por uma resolução detalhada. Bom essa é minha opinião.


moyses escreveu:(...)
Só uma pergunta para aprender limites trigonométricos que livro você recomenda ou videos na internet
(...)

 não teria como fatorar? sei la pelo método de divisão fica muito grande , e ainda sobra resto. desde já agradeço a atenção de vocês.
não teria como fatorar? sei la pelo método de divisão fica muito grande , e ainda sobra resto. desde já agradeço a atenção de vocês.
moyses escreveu:gente eu não consegui dividir através do método da chaves nem pelo método de briout ruffini.
(...)
sei la pelo método de divisão fica muito grande , e ainda sobra resto.
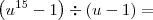


 =
=  mais e agora como simplificar , tem como? ou o limite vai dar 0 ?
mais e agora como simplificar , tem como? ou o limite vai dar 0 ?
moyses escreveu:(...) mais e agora como simplificar , tem como? (...)

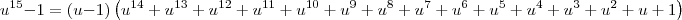




 no denominador, você colocou porque ?
no denominador, você colocou porque ?
 ,
,  eu entendi você igualou a divisão de u elevado a 15 / u-1 e o resultado . ai voce passou o divisor para outro lado multiplicando, ae assim ! não é a toa que você deve ser chamado de Professor parabens cara! Só para entender antes eu tinha o limite original, depois você me mostrou que alguns casos tem que mudar a varivel x para outra neste caso o u elevado a 15. eu tabem queria saber qunado eu preciso mudar a variavel do limite? desde ja muito obrigado rsrsrs, valeww mesmo cara,valeww tabem claudin!
eu entendi você igualou a divisão de u elevado a 15 / u-1 e o resultado . ai voce passou o divisor para outro lado multiplicando, ae assim ! não é a toa que você deve ser chamado de Professor parabens cara! Só para entender antes eu tinha o limite original, depois você me mostrou que alguns casos tem que mudar a varivel x para outra neste caso o u elevado a 15. eu tabem queria saber qunado eu preciso mudar a variavel do limite? desde ja muito obrigado rsrsrs, valeww mesmo cara,valeww tabem claudin!
moyses escreveu:Só para entender antes eu tinha o limite original, depois você me mostrou que alguns casos tem que mudar a varivel x para outra neste caso o u elevado a 15. eu tabem queria saber qunado eu preciso mudar a variavel do limite?

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
