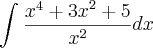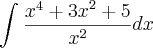por SheylaTamarossi » Sáb Out 01, 2011 19:02
por SheylaTamarossi » Sáb Out 01, 2011 19:02
Olá... Estou com dúvida nesta questão, se puderem me ajudar...
Calcular a antiderivada de:
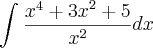
Devo integrar parte por parte, desse jeito?

Ou devo derivar a funçaõ toda?
-
SheylaTamarossi
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Jun 12, 2011 10:50
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: 3° ano
- Andamento: cursando
 por Neperiano » Sáb Out 01, 2011 19:43
por Neperiano » Sáb Out 01, 2011 19:43
Ola
Assim, se for pra integra você pode fazer isso que você fez, se for pra deriva,dai tenque sera função toda, eu só fiquei na dúvida, o que é pra fazer, antiderivada de integral é derivada?
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por MarceloFantini » Dom Out 02, 2011 15:19
por MarceloFantini » Dom Out 02, 2011 15:19
A integral é a antiderivada, ou seja, basta resolver a integral. O que você fez está certo Sheyla, agora basta enxergar como polinômios.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Neperiano » Dom Out 02, 2011 16:23
por Neperiano » Dom Out 02, 2011 16:23
Ola
Tá mas o que seria, a antiderivada da integral?
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por MarceloFantini » Dom Out 02, 2011 16:26
por MarceloFantini » Dom Out 02, 2011 16:26
Você não entendeu. A antiderivada É a integral, ou seja, antiderivada=integral.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Neperiano » Dom Out 02, 2011 16:29
por Neperiano » Dom Out 02, 2011 16:29
Ola
Eu sei, mas pelo que foi postado pelo exercíco, dá a entender que é a antiderivada da integral
SheylaTamarossi escreveu:Olá... Estou com dúvida nesta questão, se puderem me ajudar...
Calcular a antiderivada de:
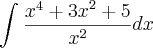
Devo integrar parte por parte, desse jeito?

Ou devo derivar a funçaõ toda?
Entende, eu sei que antiderivada é integral, mas pelo que está ali, parece outra coisa
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.