 por GustavoArtur » Qui Set 22, 2011 14:24
por GustavoArtur » Qui Set 22, 2011 14:24
Olá a todos,
Sou novo no fórum e gostaria que algum me ajudasse a encontrar a solução de uma equação diferencial parcial linear de primeira ordem.
Vou começar descrevendo o problema: tenho duas equações diferenciais que descrevem a dinâmica de um trocador de calor solar, porém a que tenho interesse em encontrar a solução é a seguinte:
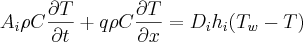
as seguintes variáveis são constantes:
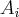
,

,

,

,
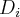
,
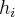
,
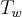
.
a variação esta em

.
Tentei fazer a resolução por um método que encontrei no livro: elements of mathematical ecology, onde se separa a solução em um produto de termos no tempo e espaço:
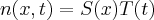
. Neste caso tem-se
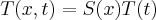
.
Com isto fiz a substituição na equação original, porém, não consegui arranjar a equação com os termos com derivadas no tempo de um lado e derivadas no espaço no outro, como sugere o autor. Gostaria, se possível, que alguem me ajudasse dando dicas ou até mesmo indicando algum material para eu me basear para encontrar a solução.
att, Gustavo
-
GustavoArtur
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Set 22, 2011 13:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por LuizAquino » Qui Set 22, 2011 23:48
por LuizAquino » Qui Set 22, 2011 23:48
GustavoArtur escreveu: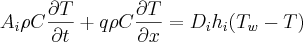
as seguintes variáveis são constantes:
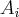
,

,

,

,
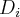
,
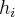
,
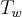
.
a variação esta em T.
Tentei fazer a resolução por um método que encontrei no livro: elements of mathematical ecology, onde se separa a solução em um produto de termos no tempo e espaço: n(x,t)=S(x)T(t).
Como você mesmo já notou, não é possível resolver essa EDP através do método de separação de variáveis.
Nesse caso, você precisa aplicar o
método das características.
Abaixo seguem duas referências onde você pode obter mais informações sobre esse método. Entretanto, com um pesquisa pela internet você deve encontrar outros materiais.
Pinchover, Yehuda; Rubinstein, Jacob.
An Introduction to Partial Differential Equations. New York: Cambridge University Press, 2005. 384 p.
The Method of Characteristics with applications to Conservation Lawshttp://www.scottsarra.org/shock/shock.html
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por MarceloFantini » Sex Set 23, 2011 00:19
por MarceloFantini » Sex Set 23, 2011 00:19
Eu me lembro que no livro Methods of Mathematical Physics do autor Richard Courant há vários métodos para resolução de EDPs, pode ser que encontre algum jeito lá. É um livro difícil, já fica o aviso.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por GustavoArtur » Sex Set 23, 2011 12:58
por GustavoArtur » Sex Set 23, 2011 12:58
ok, Vou tentar encontrar a solução pelo metodo das caracteristicas. Em breve posto a resposta se eu conseguir encontrar a solucao.
-
GustavoArtur
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Set 22, 2011 13:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Solução de uma Equação diferencial ordinaria
por thejotta » Seg Jan 14, 2013 00:03
- 0 Respostas
- 1023 Exibições
- Última mensagem por thejotta

Seg Jan 14, 2013 00:03
Cálculo: Limites, Derivadas e Integrais
-
- [Equação diferencial] Solução incorreta?
por KleinIll » Qui Set 19, 2013 15:45
- 2 Respostas
- 1708 Exibições
- Última mensagem por KleinIll

Sáb Set 21, 2013 01:15
Cálculo: Limites, Derivadas e Integrais
-
- [Equação diferencial] Região no plano com única solução
por Aliocha Karamazov » Dom Fev 26, 2012 11:52
- 1 Respostas
- 3787 Exibições
- Última mensagem por LuizAquino

Dom Fev 26, 2012 13:39
Cálculo: Limites, Derivadas e Integrais
-
- [Equação Diferencial] Grau de homogeneidade e solução geral
por kayone » Dom Set 22, 2013 17:37
- 1 Respostas
- 1660 Exibições
- Última mensagem por Man Utd

Dom Jun 15, 2014 23:49
Equações
-
- [Derivada Parcial] Pedido de ajuda para resolução
por itsdeas » Sex Nov 07, 2014 18:21
- 3 Respostas
- 3165 Exibições
- Última mensagem por young_jedi

Seg Nov 10, 2014 20:25
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
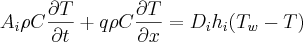
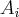 ,
,  ,
,  ,
,  ,
, 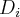 ,
, 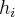 ,
, 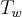 .
. .
.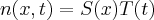 . Neste caso tem-se
. Neste caso tem-se 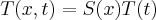 .
.








