Esse é meu primeiro tópico, então desculpe qualquer erro...
Gostaria de pedir ajuda a vocês para resolver esse exercício:
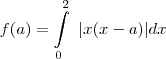 , Com
, Com  variando de:
variando de: 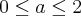
I) Encontrar

II) Encontrar o mínimo de

Obrigado desde já...

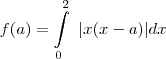 , Com
, Com  variando de:
variando de: 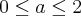




 e o
e o  variam entre 0 e 2, mas a função em si, depende do parâmetro
variam entre 0 e 2, mas a função em si, depende do parâmetro  e não do
e não do  , por isso fiquei meio confuso em resolver esse exercício.
, por isso fiquei meio confuso em resolver esse exercício.

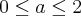 .
. .
.
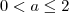 .
.
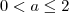 , temos que
, temos que


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes