 por caiofisico » Sáb Ago 20, 2011 22:38
por caiofisico » Sáb Ago 20, 2011 22:38
opa, tenho uma dúvida que ainda não consegui sanar
é para determinar um delta>0 para todo epsilon dado
tal que se

então
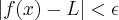

não consegui entender a explicação do livro, estou no momento tendo as primeiras aulas de calculo 1
se alguém puder me dar uma ajuda eu agradeço muito
-
caiofisico
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Sáb Ago 20, 2011 22:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por LuizAquino » Dom Ago 21, 2011 21:58
por LuizAquino » Dom Ago 21, 2011 21:58
caiofisico escreveu:(...) não consegui entender a explicação do livro (...)
O que exatamente você não entendeu na explicação?
caiofisico escreveu:(...) estou no momento tendo as primeiras aulas de calculo 1 (...)
Talvez você se interesse por dois canais no YouTube:
http://www.youtube.com/nerckiehttp://www.youtube.com/LCMAquino
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por caiofisico » Dom Ago 21, 2011 22:47
por caiofisico » Dom Ago 21, 2011 22:47
basicamente o que eu não entendi foi o lance do módulo na equação modular, eu posso por exemplo dar a resposta do delta digamos que seja 0,01/| x+1| ? resumindo posso deixar o módulo?
-
caiofisico
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Sáb Ago 20, 2011 22:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por LuizAquino » Seg Ago 22, 2011 08:43
por LuizAquino » Seg Ago 22, 2011 08:43
caiofisico escreveu:basicamente o que eu não entendi foi o lance do módulo na equação modular
Bem, na verdade não há uma
equação modular, mas sim uma
inequação modular.
caiofisico escreveu:eu posso por exemplo dar a resposta do delta digamos que seja 0,01/| x+1| ? resumindo posso deixar o módulo?
Não pode! Isso porque o delta deve ficar em função
apenas do valor de épsilon. Perceba que do modo que você escreveu o delta está em função de épsilon e de x.
Veja se o tópico abaixo lhe dá uma ideia de como fazer:
Demonstração de limitesviewtopic.php?f=120&t=4149
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por caiofisico » Seg Ago 22, 2011 19:00
por caiofisico » Seg Ago 22, 2011 19:00
era exatamente a minha dúvida, na verdade o ponto mesmo era na inequação modular, vou dar uma revisada nessa matéria.
Valeu ai pela ajuda, ate a próxima

-
caiofisico
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Sáb Ago 20, 2011 22:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Determinar o limite tendendo ao infinito.
por Arthur_Bulcao » Sex Mar 23, 2012 17:34
- 6 Respostas
- 5312 Exibições
- Última mensagem por Arthur_Bulcao

Qua Mar 28, 2012 19:08
Cálculo: Limites, Derivadas e Integrais
-
- Achar o [tex]\delta[/tex].
por filipeferminiano » Qui Ago 26, 2010 16:42
- 2 Respostas
- 2079 Exibições
- Última mensagem por filipeferminiano

Sex Ago 27, 2010 00:30
Cálculo: Limites, Derivadas e Integrais
-
- Integração e Delta
por Jhenrique » Sex Mai 24, 2013 18:19
- 2 Respostas
- 1511 Exibições
- Última mensagem por Jhenrique

Sáb Mai 25, 2013 17:13
Cálculo: Limites, Derivadas e Integrais
-
- Inequação - 2º grau com delta menor que zero
por renanrdaros » Sex Mar 25, 2011 18:27
- 8 Respostas
- 7421 Exibições
- Última mensagem por johnlaw

Dom Mar 27, 2011 16:33
Álgebra Elementar
-
- Raiz quadrada do discriminante ?Delta
por IgorFilipe » Ter Ago 23, 2011 17:13
- 7 Respostas
- 5464 Exibições
- Última mensagem por LuizAquino

Sáb Ago 27, 2011 13:07
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 então
então 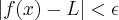


 então
então 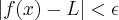









 , avisa que eu resolvo.
, avisa que eu resolvo.

