killerkill escreveu:o que me garante que entre a e b não existe um valor tal que f(x) não seja contínua?
O que vai lhe garantir é o conhecimento da função em questão.
Por exemplo, você sabe que uma reta é continua em todo o seu domínio.
Por exemplo, a função

é contínua em todo o

.
Imagine agora que você vai tomar outra função que é um "pedaço" de f. Por exemplo,
![g : [-1,\,1] \to \mathbb{R} g : [-1,\,1] \to \mathbb{R}](/latexrender/pictures/7f5baa2a4c3cf18a59395725fe081c21.png)
tal que

. Naturalmente g será contínua em [-1, 1].
Vejamos agora outro exemplo. Considere a função
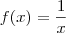
, que como você sabe é contínua em todo o
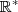
.
Se você tomar o "pedaço" de f dado por
![g : [1,\,2] \to \mathbb{R} g : [1,\,2] \to \mathbb{R}](/latexrender/pictures/6e1d21d050700a258a4dcfaa9b94f55b.png)
tal que
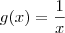
, então g é contínua em [1, 2].
Por outro lado, se você tomar o "pedaço" dado por
![h : [-1,\,1] \to \mathbb{R} h : [-1,\,1] \to \mathbb{R}](/latexrender/pictures/fc8a523a21170bac5ab6517ee541c2fb.png)
tal que

, então h não é contínua em todo o [-1, 1].
killerkill escreveu:Outra pequena dúvida, se o intervalo fosse ]a,b[ eu deveria analisar assim:
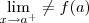
e
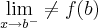
Correto?
Está incorreto. O que você deve verificar é se para todo
![c\in]a,\,b[ c\in]a,\,b[](/latexrender/pictures/c07ab444186add53ac3e865c51809d1e.png)
é valido que

.
Voltando aos exemplos anteriores, note que:
(i)
![g : ]-1,\,1[ \to \mathbb{R} g : ]-1,\,1[ \to \mathbb{R}](/latexrender/pictures/90c7ca77d3cbaa0356a0191e0f87cf7e.png)
definida por

é contínua em ]-1, 1[;
(ii)
![h : ]-1,\,1[ \to \mathbb{R} h : ]-1,\,1[ \to \mathbb{R}](/latexrender/pictures/c9f5cf00c87df50ff613c163a7114dbd.png)
definida por

não é contínua em todo o ]-1, 1[.



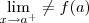
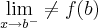


 é contínua em todo o
é contínua em todo o  .
.![g : [-1,\,1] \to \mathbb{R} g : [-1,\,1] \to \mathbb{R}](/latexrender/pictures/7f5baa2a4c3cf18a59395725fe081c21.png) tal que
tal que  . Naturalmente g será contínua em [-1, 1].
. Naturalmente g será contínua em [-1, 1].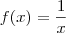 , que como você sabe é contínua em todo o
, que como você sabe é contínua em todo o 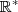 .
.![g : [1,\,2] \to \mathbb{R} g : [1,\,2] \to \mathbb{R}](/latexrender/pictures/6e1d21d050700a258a4dcfaa9b94f55b.png) tal que
tal que 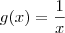 , então g é contínua em [1, 2].
, então g é contínua em [1, 2].![h : [-1,\,1] \to \mathbb{R} h : [-1,\,1] \to \mathbb{R}](/latexrender/pictures/fc8a523a21170bac5ab6517ee541c2fb.png) tal que
tal que  , então h não é contínua em todo o [-1, 1].
, então h não é contínua em todo o [-1, 1].![c\in]a,\,b[ c\in]a,\,b[](/latexrender/pictures/c07ab444186add53ac3e865c51809d1e.png) é valido que
é valido que  .
.![g : ]-1,\,1[ \to \mathbb{R} g : ]-1,\,1[ \to \mathbb{R}](/latexrender/pictures/90c7ca77d3cbaa0356a0191e0f87cf7e.png) definida por
definida por ![h : ]-1,\,1[ \to \mathbb{R} h : ]-1,\,1[ \to \mathbb{R}](/latexrender/pictures/c9f5cf00c87df50ff613c163a7114dbd.png) definida por
definida por 
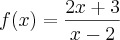

 .
.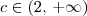 e usando as propriedades de limites mostrar que
e usando as propriedades de limites mostrar que  .
. então
então 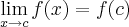 . Logo:
. Logo: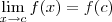

 .
. e o intervalo
e o intervalo  .
. .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
