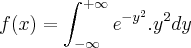
eu sei que se resolve por integração por partes!
mas ja fiz com u sendo o
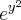 e u sendo
e u sendo 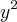 e não consigo resolver! a resposta é
e não consigo resolver! a resposta é 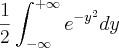

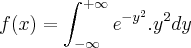
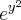 e u sendo
e u sendo 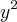 e não consigo resolver! a resposta é
e não consigo resolver! a resposta é 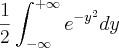



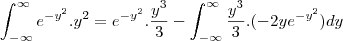
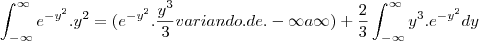
 e depois
e depois 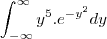 num ciclo sem fim..
num ciclo sem fim.. o que me deixou sem saída.. alguem pode me ajudar?
o que me deixou sem saída.. alguem pode me ajudar?
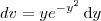 e não
e não 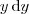 . Tente fazer essa mudança.
. Tente fazer essa mudança.

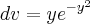 tenho entao q
tenho entao q 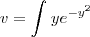 ai faz a integração normal sem os limites por enquanto??
ai faz a integração normal sem os limites por enquanto??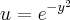

 . Lembre-se que sempre é possível fazer uma integral indefinida, encontrar a primitiva e apenas depois voltar a integral normal colocando-se limites de integração e igualando à primitiva avaliada nos limites dados.
. Lembre-se que sempre é possível fazer uma integral indefinida, encontrar a primitiva e apenas depois voltar a integral normal colocando-se limites de integração e igualando à primitiva avaliada nos limites dados.


q vc fez.. eu tava errando aí mesmo pq essa integral sem o y vai ser a integral de gauss neh isso? q vai ser a raiz de pi.. e depois eu sei q isso:MarceloFantini escreveu:Com. Lembre-se que sempre é possível fazer uma integral indefinida, encontrar a primitiva e apenas depois voltar a integral normal colocando-se limites de integração e igualando à primitiva avaliada nos limites dados.
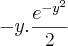 variando de
variando de  é zero.. mas eu tambem nao entendo o porque.. ja que fica assim:
é zero.. mas eu tambem nao entendo o porque.. ja que fica assim:

 e não o integrando.
e não o integrando.



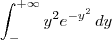 é chamada de Integral Imprópria.
é chamada de Integral Imprópria.
![\int_t^0 y^2e^{-y^2}\,dy = \left[-\frac{y}{2}e^{-y^2}\right]_t^0 - \int_t^0 -\frac{1}{2} e^{-y^2}\,dy \int_t^0 y^2e^{-y^2}\,dy = \left[-\frac{y}{2}e^{-y^2}\right]_t^0 - \int_t^0 -\frac{1}{2} e^{-y^2}\,dy](/latexrender/pictures/c8182daad63bb253af9de370703e424f.png)
![\int_0^t y^2e^{-y^2}\,dy = \left[-\frac{y}{2}e^{-y^2}\right]_0^t - \int_0^t -\frac{1}{2} e^{-y^2}\,dy \int_0^t y^2e^{-y^2}\,dy = \left[-\frac{y}{2}e^{-y^2}\right]_0^t - \int_0^t -\frac{1}{2} e^{-y^2}\,dy](/latexrender/pictures/5681872153507bc9e6d08bca374a5ba7.png)


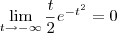
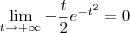



MarceloFantini escreveu:Lembre-se que sempre é possível fazer uma integral indefinida, encontrar a primitiva e apenas depois voltar a integral normal colocando-se limites de integração e igualando à primitiva avaliada nos limites dados
 é um exemplo disso. Leia um pouco sobre isso em:
é um exemplo disso. Leia um pouco sobre isso em:
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes

 .
.
 :
: