 por alexandreredefor » Dom Jul 17, 2011 18:23
por alexandreredefor » Dom Jul 17, 2011 18:23
PARA QUAIS VALORES DE X A FUNÇÃO G É CONTINUA?
G(X)= {0, SE X É RACIONAL
{ X, SE X É IRRACIONAL
obs: não consegui utilizar uma chave só.
tive uma prova e não consegui resolver vou ter prova substituta sera que pode me auxiliar...
ou me indicar algum video que tem o assunto
-
alexandreredefor
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sex Jul 15, 2011 10:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por Molina » Dom Jul 17, 2011 22:26
por Molina » Dom Jul 17, 2011 22:26
Boa noite, Alexandre.
Vou dar a ideia de como eu pensaria nesta questão e quero ver se você chega a mesma conclusão que eu:
Se imaginarmos os números reais como uma reta, teremos que cada ponto que forma esta reta são os números reais. Alguns pontos são os racionais e outros pontos são os irracionais. A união dos dois conjuntos de pontos formará a reta (

). Se retirarmos, por exemplo, os números irracionais será possível observar alguns "buracos" nesta reta. O restante que permanece na reta são os números racionais.
Um esboço disso seria:
______ _______ ____ _ ___ ____ _____________ ___ _ ____________ _ _____ ______________ _ _ ____
Colocando este esboço num sistema de coordenadas xy e esta reta com buracos sobre o eixo x, representaria parte do nosso problema em questão, pois para todo número racional, temos que a função vale 0. Falta saber o que fazer com esses pontos que retiramos.
Lembre-se que para uma função ser contínua ela não tem "buracos", ou seja, temos que desenhar toda a função "sem tirar o lápis do papel".
Então, quais os valores que esses pontos com "buracos" devem assumir para que esses "buracos" não existam mais sobre esta reta?


Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por MarceloFantini » Seg Jul 18, 2011 02:37
por MarceloFantini » Seg Jul 18, 2011 02:37
É impossível esboçar essa função, visto que todo intervalo real contém um número infinitos de números racionais e irracionais.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Seg Jul 18, 2011 11:11
por LuizAquino » Seg Jul 18, 2011 11:11
Temos a função:

Note que
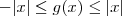
.
Como
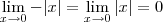
, pelo Teorema do Sanduíche segue que
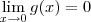
. Por outro lado, sabemos que g(0) = 0.
Portanto,
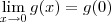
. Isso é o mesmo que dizer que g é contínua em x = 0.
Tome agora qualquer real
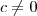
e qualquer real

. No intervalo

existem infinitos racionais e infinitos irracionais.
Considere que c seja irracional. Existem infinitos x racionais tais que

e
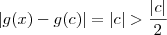
.
Por outro lado, considere que c seja racional. Existem infinitos x irracionais tais que

e

.
Em resumo: existem infinitos números x tais que

e

.
Logo,
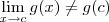
. Isso é o mesmo que dizer que g não é contínua em x = c (lembrando-se que tomamos qualquer real
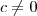
).
A conclusão final disso tudo é que a função g é contínua apenas para x = 0.
Observaçãoalexandreredefor escreveu:obs: não consegui utilizar uma chave só.
Para colocar apenas uma chave, use o comando LaTeX:
- Código: Selecionar todos
[tex]\begin{cases} caso_1 \\ caso_2 \\ caso_3 \\ \vdots \end{cases}[/tex]
O resultado desse comando é:

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Molina » Seg Jul 18, 2011 11:42
por Molina » Seg Jul 18, 2011 11:42
Bom dia!
MarceloFantini escreveu:É impossível esboçar essa função, visto que todo intervalo real contém um número infinitos de números racionais e irracionais.
Um esboço seria desenhar uma retas com alguns buracos, representando apenas os números racionais e os faltantes seriam os números irracionais.
Este esboço seria apenas para chegar a conclusão que para ser contínua,

.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função continua
por Amparo » Dom Mar 09, 2008 16:14
- 1 Respostas
- 3922 Exibições
- Última mensagem por admin

Qui Mar 13, 2008 12:52
Funções
-
- Função Contínua
por Ana Maria da Silva » Sex Mar 14, 2014 18:55
- 1 Respostas
- 1597 Exibições
- Última mensagem por Russman

Sáb Mar 15, 2014 10:45
Cálculo: Limites, Derivadas e Integrais
-
- [Função continua]
por stepg_ » Dom Set 14, 2014 13:41
- 1 Respostas
- 1667 Exibições
- Última mensagem por jcmatematica

Qui Set 25, 2014 23:27
Cálculo: Limites, Derivadas e Integrais
-
- Função contínua
por felipe_pereira96 » Qua Jan 27, 2016 12:17
- 1 Respostas
- 1791 Exibições
- Última mensagem por adauto martins

Qui Jan 28, 2016 10:00
Funções
-
- Domínio função contínua
por emanes » Seg Out 01, 2012 09:19
- 3 Respostas
- 2070 Exibições
- Última mensagem por MarceloFantini

Seg Out 01, 2012 10:04
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 ). Se retirarmos, por exemplo, os números irracionais será possível observar alguns "buracos" nesta reta. O restante que permanece na reta são os números racionais.
). Se retirarmos, por exemplo, os números irracionais será possível observar alguns "buracos" nesta reta. O restante que permanece na reta são os números racionais. 




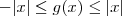 .
.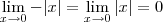 , pelo Teorema do Sanduíche segue que
, pelo Teorema do Sanduíche segue que 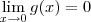 . Por outro lado, sabemos que g(0) = 0.
. Por outro lado, sabemos que g(0) = 0. 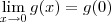 . Isso é o mesmo que dizer que g é contínua em x = 0.
. Isso é o mesmo que dizer que g é contínua em x = 0.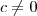 e qualquer real
e qualquer real  . No intervalo
. No intervalo  existem infinitos racionais e infinitos irracionais.
existem infinitos racionais e infinitos irracionais. e
e 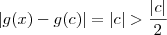 .
. .
. .
.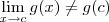 . Isso é o mesmo que dizer que g não é contínua em x = c (lembrando-se que tomamos qualquer real
. Isso é o mesmo que dizer que g não é contínua em x = c (lembrando-se que tomamos qualquer real 
 .
.





