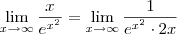por Piva » Qui Jun 30, 2011 18:29
por Piva » Qui Jun 30, 2011 18:29
Alguem pode me ajudar com o limite:
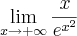
e

Eu faço o l'hospital mas continua a dar uma indeterminação....
podem me ajudar?
obrigado!
-
Piva
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Jun 29, 2011 18:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por ant_dii » Qui Jun 30, 2011 19:48
por ant_dii » Qui Jun 30, 2011 19:48
Quando você aplica L'hospital, o limite fica
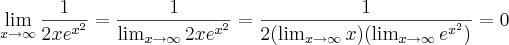
.
Da mesma forma quando

,

.
Espero ter ajudado.
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por MarceloFantini » Qui Jun 30, 2011 19:52
por MarceloFantini » Qui Jun 30, 2011 19:52
Vamos aplicar L'Hospital na primeira:
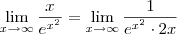
Note que aqui já não há mais indeterminação, pois o numerador é constante e o denominador vai para infinito, logo o limite é zero.
No segundo limite, você chegará ao mesmo resultado, porém note que você terá menos infinito vezes mais infinito que é menos infinito, mas também zera.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Claudin » Sex Jul 01, 2011 03:55
por Claudin » Sex Jul 01, 2011 03:55
Seria o mesmo limite representado neste tópico ou não?
viewtopic.php?f=120&t=5270"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Piva » Sáb Jul 02, 2011 19:30
por Piva » Sáb Jul 02, 2011 19:30
Não claudin, no seu topico não tem o e. Era isso mesmo, não tinha percebido minha falha ao fazer o l'hospital.
obrigado
-
Piva
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Jun 29, 2011 18:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por Fabio Cabral » Dom Jul 03, 2011 02:38
por Fabio Cabral » Dom Jul 03, 2011 02:38
Piva,
Costumo analisar esse tipo de questão antes de fazer qualquer cálculo. Verificar indeterminação (se há), tipo de indeterminação, se é contínua ou descontínua no ponto (etc), enfim..
Isso ajuda a determinar qual propriedade será mais vantajosa aplicar para resolver.
Fica a dica!
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limite complicado
 por sergiosilva » Qua Jan 05, 2011 23:25
por sergiosilva » Qua Jan 05, 2011 23:25
- 2 Respostas
- 1675 Exibições
- Última mensagem por victoreis1

Sex Jan 07, 2011 00:04
Cálculo: Limites, Derivadas e Integrais
-
- Juros Compostos Complicado...
por gustavowelp » Sex Nov 19, 2010 08:20
- 4 Respostas
- 2278 Exibições
- Última mensagem por gustavowelp

Sex Nov 19, 2010 15:48
Matemática Financeira
-
- [DUV] Somatório Binomial Complicado
por Imscatman » Qui Mar 17, 2011 18:27
- 3 Respostas
- 2301 Exibições
- Última mensagem por Imscatman

Qui Mar 17, 2011 19:00
Binômio de Newton
-
- [Álgebra Elementar] Se x=a.y/b, y=? Um pouco mais complicado
 por Zicra » Qua Mar 30, 2016 18:47
por Zicra » Qua Mar 30, 2016 18:47
- 4 Respostas
- 5058 Exibições
- Última mensagem por Zicra

Seg Abr 11, 2016 17:56
Álgebra Elementar
-
- Raciocínio Lógico "Um Tanto" Complicado
por gustavowelp » Dom Jun 27, 2010 22:39
- 2 Respostas
- 1586 Exibições
- Última mensagem por gustavowelp

Dom Jun 27, 2010 23:33
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
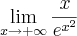


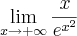


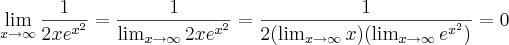 .
. ,
,  .
.