





![y = 2a^2 [sen(Pi - a).cos(Pi - a) + sen(Pi - a)] /9 y = 2a^2 [sen(Pi - a).cos(Pi - a) + sen(Pi - a)] /9](/latexrender/pictures/9a3980c85bb3ac53b51b6f2a657f22c9.png)
![[sen(Pi - a).cos(Pi - a) + sen(Pi - a)] ' [sen(Pi - a).cos(Pi - a) + sen(Pi - a)] '](/latexrender/pictures/12b943f403b054b66b44ce694e29cb62.png) . Dentro dessa derivada tem outro produto, dai fico sem saber como proceder, como aplicar a regra da cadeia corretamente.
. Dentro dessa derivada tem outro produto, dai fico sem saber como proceder, como aplicar a regra da cadeia corretamente.

![y= 2a^2 [2[cos(Pi -a)]^2 + cos(Pi - a) -1] y= 2a^2 [2[cos(Pi -a)]^2 + cos(Pi - a) -1]](/latexrender/pictures/e9f246146c71692f8a1988c14e27d2a5.png)

![A(\alpha) = \frac{a^2}{9}[\cos(\pi - \alpha) + 1]\textrm{sen}\, (\pi - \alpha) A(\alpha) = \frac{a^2}{9}[\cos(\pi - \alpha) + 1]\textrm{sen}\, (\pi - \alpha)](/latexrender/pictures/385eed659c85df30319fff30056e2eaf.png) .
.![A^\prime(\alpha) = \frac{a^2}{9}[\textrm{sen}^2\, (\pi - \alpha) - \cos^2(\pi - \alpha) - \cos(\pi - \alpha)] A^\prime(\alpha) = \frac{a^2}{9}[\textrm{sen}^2\, (\pi - \alpha) - \cos^2(\pi - \alpha) - \cos(\pi - \alpha)]](/latexrender/pictures/05d6154f17c3b98fc1a3f37fea5023df.png) .
.![A^\prime(\alpha) = \frac{a^2}{9}[1-2\cos^2(\pi - \alpha) - \cos(\pi - \alpha)] A^\prime(\alpha) = \frac{a^2}{9}[1-2\cos^2(\pi - \alpha) - \cos(\pi - \alpha)]](/latexrender/pictures/aba8a17653fa1eb649ba7ae7ee573767.png) .
.

 são
são 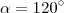 e
e 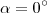 .
.

 .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)