 por [icaro] » Sáb Mai 21, 2011 19:06
por [icaro] » Sáb Mai 21, 2011 19:06
Não estou conseguindo resolver as seguintes derivadas:
A)
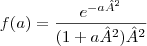
B)
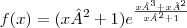
c)
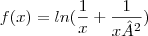
Tentei, mas só chego em resultados errados

-
[icaro]
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Mar 09, 2011 00:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ciências e tecnologia
- Andamento: cursando
 por LuizAquino » Dom Mai 22, 2011 11:30
por LuizAquino » Dom Mai 22, 2011 11:30
Primeiro, vamos arrumar o que você escreveu:
a)
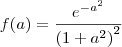
b)
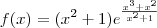
c)
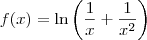
Vale destacar que o seu erro ao usar o LaTeX foi escrever x² e x³ ao invés de x^2 e x^3. Ou seja:
não use os atalhos de teclado para escrever as potências.
Quanto aos exercícios, quais foram as suas dificuldades ao resolver essas derivadas?
Muito provavelmente você está errando a aplicação da regra da cadeia.
Veja, por exemplo, a solução do primeiro exercício:
![f^\prime(a)=\frac{\left({e}^{-a^2}\right)^\prime \left(1+a^2\right)^2 - {e}^{-a^2}\left[\left(1+a^2\right)^2\right]^\prime}{\left[\left(1+a^2\right)^2\right]^2} f^\prime(a)=\frac{\left({e}^{-a^2}\right)^\prime \left(1+a^2\right)^2 - {e}^{-a^2}\left[\left(1+a^2\right)^2\right]^\prime}{\left[\left(1+a^2\right)^2\right]^2}](/latexrender/pictures/8654db3fe9635fc6f806069f4bd0c030.png)
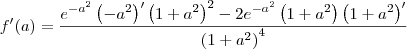
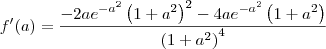
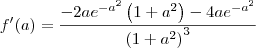
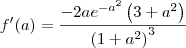
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por [icaro] » Dom Mai 22, 2011 12:54
por [icaro] » Dom Mai 22, 2011 12:54
Eu comecei atribuindo
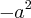
como "u" e utilizei os operadores
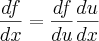
chegando ao resultado de
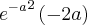
depois apliquei a regra da cadeia chegando a
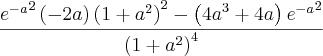
-
[icaro]
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Mar 09, 2011 00:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ciências e tecnologia
- Andamento: cursando
 por LuizAquino » Dom Mai 22, 2011 13:17
por LuizAquino » Dom Mai 22, 2011 13:17
Sendo assim, a sua dúvida está em algo mais básico ainda. Você não soube efetuar a fatoração e em seguida fazer as simplificações.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvidas em Limites e derivadas
por babiiimbaa » Dom Ago 29, 2010 20:02
- 0 Respostas
- 1393 Exibições
- Última mensagem por babiiimbaa

Dom Ago 29, 2010 20:02
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Dificuldade para calcular derivadas CDI 1
por srmai » Seg Nov 04, 2013 01:21
- 0 Respostas
- 2261 Exibições
- Última mensagem por srmai

Seg Nov 04, 2013 01:21
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Interpretação de derivadas e funções
por vinik1 » Qua Out 12, 2011 16:03
- 5 Respostas
- 7473 Exibições
- Última mensagem por vinik1

Qui Out 13, 2011 10:48
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Derivadas em pontos dados
por MarlonMO250 » Sex Mar 01, 2013 21:02
- 6 Respostas
- 4943 Exibições
- Última mensagem por Russman

Sáb Mar 02, 2013 03:42
Cálculo: Limites, Derivadas e Integrais
-
- (derivadas) derivadas com raiz como se faz
por jana garcia » Qua Jun 25, 2014 00:28
- 1 Respostas
- 2963 Exibições
- Última mensagem por e8group

Qua Jun 25, 2014 01:13
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
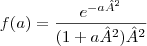
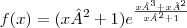
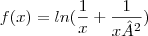


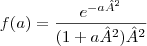
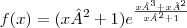
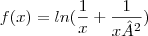


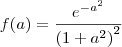
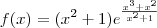
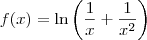
![f^\prime(a)=\frac{\left({e}^{-a^2}\right)^\prime \left(1+a^2\right)^2 - {e}^{-a^2}\left[\left(1+a^2\right)^2\right]^\prime}{\left[\left(1+a^2\right)^2\right]^2} f^\prime(a)=\frac{\left({e}^{-a^2}\right)^\prime \left(1+a^2\right)^2 - {e}^{-a^2}\left[\left(1+a^2\right)^2\right]^\prime}{\left[\left(1+a^2\right)^2\right]^2}](/latexrender/pictures/8654db3fe9635fc6f806069f4bd0c030.png)
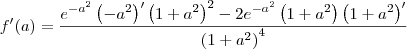
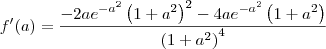
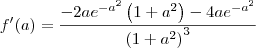
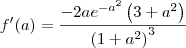

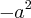 como "u" e utilizei os operadores
como "u" e utilizei os operadores 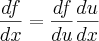 chegando ao resultado de
chegando ao resultado de 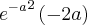
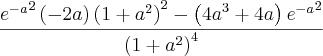


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
