 por sandra silva » Seg Set 29, 2008 20:01
por sandra silva » Seg Set 29, 2008 20:01
Me ajudaem ae umaurgencia
provar que:
[sen(x)]^(5) = cos(x)
-
sandra silva
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Ter Ago 26, 2008 22:00
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: lic em matematica
- Andamento: cursando
 por Molina » Ter Set 30, 2008 00:53
por Molina » Ter Set 30, 2008 00:53
Boa noite, Sandra.
Nunca fiz essa prova elevada a 5, apenas provei que
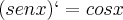
. Vou postar aqui, espero que te ajude:
![\frac{d}{dx}[senx]\Rightarrow \lim_{h\rightarrow 0}\frac{sen(x+h)-sen(x)}{h}= \lim_{h\rightarrow 0} \frac{sen(x)cos(h)+sen(h)cos(x)-sen(x)}{h}= \lim_{h\rightarrow 0} \frac{sen(x)(cos(h)-1)+sen(h)cos(x)}{h}=\lim_{h\rightarrow 0} \frac{sen(x)(cos(h)-1)}{h} + \lim_{h\rightarrow 0} \frac{sen(h)cos(x)}{h}= sen(x) \lim_{h\rightarrow 0} \frac{(cos(h)-1)}{h} + cos(x) \lim_{h\rightarrow 0} \frac{sen(h)}{h} \frac{d}{dx}[senx]\Rightarrow \lim_{h\rightarrow 0}\frac{sen(x+h)-sen(x)}{h}= \lim_{h\rightarrow 0} \frac{sen(x)cos(h)+sen(h)cos(x)-sen(x)}{h}= \lim_{h\rightarrow 0} \frac{sen(x)(cos(h)-1)+sen(h)cos(x)}{h}=\lim_{h\rightarrow 0} \frac{sen(x)(cos(h)-1)}{h} + \lim_{h\rightarrow 0} \frac{sen(h)cos(x)}{h}= sen(x) \lim_{h\rightarrow 0} \frac{(cos(h)-1)}{h} + cos(x) \lim_{h\rightarrow 0} \frac{sen(h)}{h}](/latexrender/pictures/2e692a5db833df60e5d3ca9ae9e71789.png)
agora vamos por parte:

levamos em consideração o limite fundamental

voltando a nossa conta:
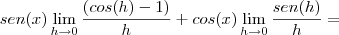
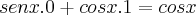
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por sandra silva » Ter Set 30, 2008 06:40
por sandra silva » Ter Set 30, 2008 06:40
Ola, Molina muito obrigada,ja estava de cabelos branço.
voccê de ajuda matematica e muito importante para a minha caminhada que e longa.
bj sandra
-
sandra silva
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Ter Ago 26, 2008 22:00
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: lic em matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12552 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [derivada] derivada pela definição da secante
por TheKyabu » Sáb Out 27, 2012 23:24
- 2 Respostas
- 10881 Exibições
- Última mensagem por TheKyabu

Dom Out 28, 2012 11:44
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Com duas variáveis e derivada mista
por leticiaeverson » Dom Abr 22, 2018 00:39
- 3 Respostas
- 13186 Exibições
- Última mensagem por Gebe

Dom Abr 22, 2018 17:11
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada]derivada de função de raiz cúbica
por armando » Sáb Jul 20, 2013 15:22
- 4 Respostas
- 14793 Exibições
- Última mensagem por armando

Dom Jul 21, 2013 22:17
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] DERIVADA POR DEFINIÇÃO DA RAIZ DO MÓDULO DE X
por Matheusgdp » Qua Set 16, 2015 04:07
- 2 Respostas
- 5111 Exibições
- Última mensagem por Matheusgdp

Qui Set 17, 2015 18:31
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



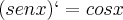 . Vou postar aqui, espero que te ajude:
. Vou postar aqui, espero que te ajude:![\frac{d}{dx}[senx]\Rightarrow \lim_{h\rightarrow 0}\frac{sen(x+h)-sen(x)}{h}= \lim_{h\rightarrow 0} \frac{sen(x)cos(h)+sen(h)cos(x)-sen(x)}{h}= \lim_{h\rightarrow 0} \frac{sen(x)(cos(h)-1)+sen(h)cos(x)}{h}=\lim_{h\rightarrow 0} \frac{sen(x)(cos(h)-1)}{h} + \lim_{h\rightarrow 0} \frac{sen(h)cos(x)}{h}= sen(x) \lim_{h\rightarrow 0} \frac{(cos(h)-1)}{h} + cos(x) \lim_{h\rightarrow 0} \frac{sen(h)}{h} \frac{d}{dx}[senx]\Rightarrow \lim_{h\rightarrow 0}\frac{sen(x+h)-sen(x)}{h}= \lim_{h\rightarrow 0} \frac{sen(x)cos(h)+sen(h)cos(x)-sen(x)}{h}= \lim_{h\rightarrow 0} \frac{sen(x)(cos(h)-1)+sen(h)cos(x)}{h}=\lim_{h\rightarrow 0} \frac{sen(x)(cos(h)-1)}{h} + \lim_{h\rightarrow 0} \frac{sen(h)cos(x)}{h}= sen(x) \lim_{h\rightarrow 0} \frac{(cos(h)-1)}{h} + cos(x) \lim_{h\rightarrow 0} \frac{sen(h)}{h}](/latexrender/pictures/2e692a5db833df60e5d3ca9ae9e71789.png)


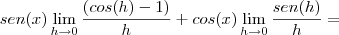
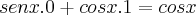


![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.