Paulod22 escreveu:Fiz do jeito que você falou, multipliquei e dividi pelo conjugado.
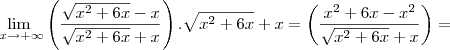
Dividindo tudo por x:
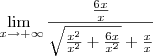
=

Apenas uma correção. No desenvolvimento de um limite você sempre deve escrever a notação "lim" em cada passo, exceto no último quando o limite é calculado. Isto é, ao invés de escrever
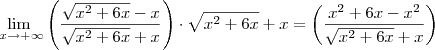
você deve escrever
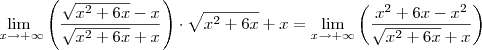
.
Paulod22 escreveu:Mas ainda tenho dúvida quanto à divisão. Quero entender direito para não errar mais nisso.
Pelo que eu pude perceber, se eu dividir tudo por x eu estarei alterando a equação.
Então, a resolução do limite abaixo também está errada? (Esse limite ai eu tinha resolvido anteriormente, mas como o resultado bateu eu nem desconfiei que tava errado

)

Sim, está errada. Foi apenas uma mera coincidência você ter obtido a reposta correta. Perceba como no exemplo anterior você usou a mesma estratégia e havia chegado na reposta errada do exercício. Além disso, novamente você não usou a notação adequada em cada passo.
Vejamos a solução correta.
Como o cosseno é uma função contínua em todo o seu domínio, podemos "retirá-la" do limite. Além disso, vamos multiplicar e dividir a expressão no limite por

.

Após aplicar o produto notável no numerador, nós dividimos tanto o numerador quanto o denominador por

. Após as simplificações, ficamos com:


É interessante destacar que nesse exercício se tivéssemos dividido o numerador e o denominador por
x ao invés de

, não poderíamos resolver o limite, pois teríamos uma indeterminação do tipo 0/0. Veja como ficaria:
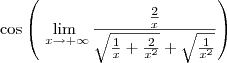
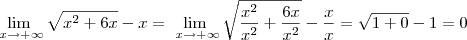


 . Mas,
. Mas, 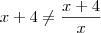 (exceto para x=1 ou x=-4).
(exceto para x=1 ou x=-4).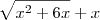 . Tente fazer e poste aqui a sua solução.
. Tente fazer e poste aqui a sua solução.
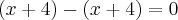

 .
.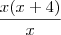 .
.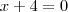 e
e  possuem a mesma solução: x=-4.
possuem a mesma solução: x=-4. e
e  possuem soluções distintas!
possuem soluções distintas!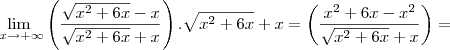
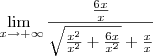 =
= 
 )
)
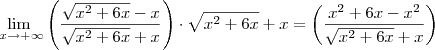 você deve escrever
você deve escrever 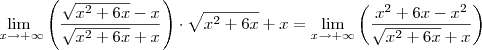 .
.
 .
.
 . Após as simplificações, ficamos com:
. Após as simplificações, ficamos com:

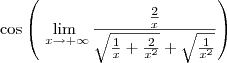
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
