 no intervalo
no intervalo 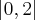
e se função for ;
 no intervalo
no intervalo 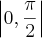
Ajude-me a entender essas questões.
Desde de já obrigada!

 no intervalo
no intervalo 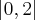
 no intervalo
no intervalo 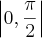

![A = 2\pi\int_a^b f(x)\sqrt{1+[f^\prime(x)]^2}\,dx A = 2\pi\int_a^b f(x)\sqrt{1+[f^\prime(x)]^2}\,dx](/latexrender/pictures/4663b68b51f64c711fd9fdebffdbf672.png) ,
,Calcular a área da superfície dada por:
1) Rotação deem torno do eixo x no intervalo [0, 2].
2) Rotação deem torno do eixo x no intervalo
.

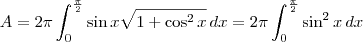
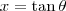 . Já na segunda, você vai precisar usar a identidade
. Já na segunda, você vai precisar usar a identidade  .
.
Isla escreveu:como faço para calcular a area a superficie,que é obtida pela revolução do grafico da função dada num intervalo de:no intervalo
e se função for ;no intervalo
Ajude-me a entender essas questões.
Desde de já obrigada!
![\int\frac{{x}^{2}}{2\sqrt[]{1+{x}^{2}}} \int\frac{{x}^{2}}{2\sqrt[]{1+{x}^{2}}}](/latexrender/pictures/4eae5dffcab4bb03cb70b471dace7b9c.png)
![=(\frac{{sen}^{-1})-x\sqrt[]{{(x}^{2}+1})}{4+c} =(\frac{{sen}^{-1})-x\sqrt[]{{(x}^{2}+1})}{4+c}](/latexrender/pictures/3c98da3a232be4ab307bfaa570c6607b.png)
![\int_{0}^{2}\frac{{x}^{2}}{2\sqrt[]{(1+{x}^{2})}}=\frac{{sen}^{-1}-2\sqrt[]{{2}^{2}+1}}{4} \int_{0}^{2}\frac{{x}^{2}}{2\sqrt[]{(1+{x}^{2})}}=\frac{{sen}^{-1}-2\sqrt[]{{2}^{2}+1}}{4}](/latexrender/pictures/80ff672f103de08d29deeea60fcfdbdd.png)

Isla escreveu:Por favor me ajude a concluir meu raciocinio:
E agora vou para onde?
Estou no caminho correto?
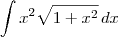 .
.

LuizAquino escreveu:2)
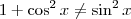 . Na verdade, sabemos que a relação correta é
. Na verdade, sabemos que a relação correta é  .
.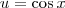 . Em seguida, será necessário usar a substituição trigonométrica
. Em seguida, será necessário usar a substituição trigonométrica 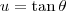 .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.