g(x)= (2+x)*e^x
Mostre que g'(x)=(3+x)e^x
Comecei a fazer pela regra do produto.
g'(x)= (2+x)' * e^x + (2+x) * (e^x)'
g'(x)= 1*e^x + (2+x) * 1* (e^x)
g'(x)= e^x + (2+x) * (e^x)
Mas não consigo provar o que é pedido.
Alguém ajuda? Obrigado.



 = f'(x)=
= f'(x)=

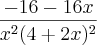
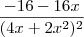
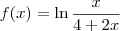 , calcule f'.
, calcule f'.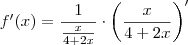

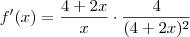
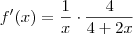

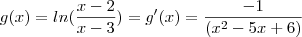
 =
=  '
'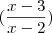
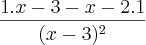

 com
com 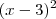

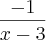
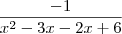
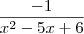
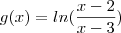 , então
, então 
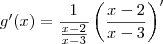
![g^\prime (x) = \frac{x-3}{x-2} \left[\frac{1\cdot(x-3)-(x-2)\cdot 1}{(x-3)^2}\right] g^\prime (x) = \frac{x-3}{x-2} \left[\frac{1\cdot(x-3)-(x-2)\cdot 1}{(x-3)^2}\right]](/latexrender/pictures/c7ea80086040152d739754365d444de5.png)
![g^\prime (x) = \frac{x-3}{x-2} \left[\frac{-1}{(x-3)^2}\right] g^\prime (x) = \frac{x-3}{x-2} \left[\frac{-1}{(x-3)^2}\right]](/latexrender/pictures/04e87793daaf171764631366016612a2.png)

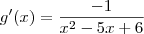

 e não
e não 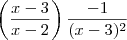 como era esperado.
como era esperado.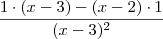 .
.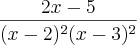
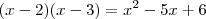 ? Basta lembrar disso e você termina a questão.
? Basta lembrar disso e você termina a questão.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)