O limite é o seguinte :
![\lim_{x\to_{-\infty}}\frac{\sqrt[2]{4x^2 + 7}}{\sqrt[3]{x^3+3x^2+1}}](/latexrender/pictures/f20ebc39e321c651302164df9021cfec.png "\lim_{x\to_{-\infty}}\frac{\sqrt[2]{4x^2 + 7}}{\sqrt[3]{x^3+3x^2+1}}")
...
Conforme eu fui fazendo l' hopital foram aparecendo mais denominadores com raizes e ao invés de facilitar fui complicando !
Abraço,
Otávio
por OtavioBonassi » Sex Jan 07, 2011 01:57
por Pedro123 » Sex Jan 07, 2011 02:02
por VtinxD » Sex Jan 07, 2011 12:35
![\lim_{\infty}=\frac{\sqrt[6]{{(4{x}^{2}+7)}^{3}}}{\sqrt[6]{{({x}^{3}+3{x}^{2}+1)}^{2}}}](/latexrender/pictures/f0e5ccc1ad47bf5fb12fc4763b451631.png "\lim_{\infty}=\frac{\sqrt[6]{{(4{x}^{2}+7)}^{3}}}{\sqrt[6]{{({x}^{3}+3{x}^{2}+1)}^{2}}}")
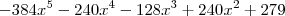.Agora só usar as derivadas para descobrir , que ele só possui uma raiz real e quando x tende a -oo a função tende a +oo também.Você tambem pode perceber que -384x^5-128x^3+240x^2 cresce muito mais rapidamente que -240x^4 quando tendidos a numeros negativamente grandes ,tendendo assim para +oo.por OtavioBonassi » Sex Jan 07, 2011 16:14
por VtinxD » Sex Jan 07, 2011 16:56
![1-\sqrt[]{3}i](/latexrender/pictures/e92b072d503cf2e7961c2025af97f522.png "1-\sqrt[]{3}i")
.Agora qual esta certo eu não sei dizer mas tenho quase certeza de que o meu anterior esta errado.por OtavioBonassi » Sex Jan 07, 2011 17:00
por Renato_RJ » Sex Jan 07, 2011 22:56
![\lim_{x\rightarrow\infty}{\frac{\sqrt[6]{(4*x^2+7)^3}}{\sqrt[6]{(x^3+3*x^2+1)^2}}}](/latexrender/pictures/419dba74d814fe93a1594c8ae04e4b6f.png "\lim_{x\rightarrow\infty}{\frac{\sqrt[6]{(4*x^2+7)^3}}{\sqrt[6]{(x^3+3*x^2+1)^2}}}")
![\lim_{x\rightarrow\infty}{\sqrt[6]{\frac{64*x^6+336*x^4+588*x^2+343}{x^6+6*x^5+9*x^4+2*x^3+6*x^2+1}}}](/latexrender/pictures/acc06e6670fffed0094bda6905898a1a.png "\lim_{x\rightarrow\infty}{\sqrt[6]{\frac{64*x^6+336*x^4+588*x^2+343}{x^6+6*x^5+9*x^4+2*x^3+6*x^2+1}}}")
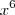temos:![\lim_{x\rightarrow\infty}{\sqrt[6]{\frac{(64+\frac{336}{x^2}+\frac{588}{x^4}+\frac{343}{x^6})}{(1+\frac{6}{x}+\frac{9}{x^2}+\frac{2}{x^3}+\frac{6}{x^4}+\frac{1}{x^6})}}}](/latexrender/pictures/8d118446baed581474573fa2b9b2951d.png "\lim_{x\rightarrow\infty}{\sqrt[6]{\frac{(64+\frac{336}{x^2}+\frac{588}{x^4}+\frac{343}{x^6})}{(1+\frac{6}{x}+\frac{9}{x^2}+\frac{2}{x^3}+\frac{6}{x^4}+\frac{1}{x^6})}}}")
![\sqrt[6]{64} \, \Rightarrow \sqrt[6]{2^6} \, \Rightarrow 2](/latexrender/pictures/eed7efa8af20ed08b2bcf46cca6505ef.png "\sqrt[6]{64} \, \Rightarrow \sqrt[6]{2^6} \, \Rightarrow 2")
por MarceloFantini » Sex Jan 07, 2011 23:32
![\sqrt[6]{64} = 2](/latexrender/pictures/5d764e37b9fdb3722192b6ee8bfc0fbc.png "\sqrt[6]{64} = 2")
.
por OtavioBonassi » Sáb Jan 08, 2011 00:00
por Renato_RJ » Sáb Jan 08, 2011 01:51
![\sqrt[6]{64}](/latexrender/pictures/3a376bbb046aaf386dfaf17513ee9f7c.png "\sqrt[6]{64}")
no fim do limite (mesmo que o limite tenha tendência pela esquerda ou direita), só que eu demorei um tempo bem considerado para resolver... O que aconteceu comigo, foi que segui da dica do colega VtinxD para colocar os dois polinômios em uma raiz de mesma potência (facilitando as contas).por OtavioBonassi » Sáb Jan 08, 2011 09:30
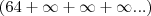e assim vai . Agora ,nao sei se a raiz da soma de infinitos dividido pela raiz da soma dos infinitos é uma indeterminação ou não.por Renato_RJ » Sáb Jan 08, 2011 12:15
Voltar para Cálculo: Limites, Derivadas e Integrais
por Raphaela_sf » Qui Abr 05, 2012 19:26
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes