 por macburn » Qua Nov 03, 2010 19:14
por macburn » Qua Nov 03, 2010 19:14
Olá pessoal,
Boa noite, tudo bom? Tenho a seguinte equação:
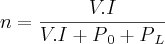
Como seria a derivada desta equação em relação a V.I
P.S.: pessoal, V.I é a equação de potência elétrica

Deixo aqui meus agradecimentos pessoal!
Abraços!
-
macburn
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Nov 02, 2010 14:36
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por macburn » Qua Nov 03, 2010 19:38
por macburn » Qua Nov 03, 2010 19:38
Olá pessoal,
Olá Fantini. Muito bom meu nobre! Você por acaso teria um material de consulta para que eu pudesse dar uma olhada, e ver como foi resolvido? meio que um passo-a-passo!
Desde já meus sinceros agradecimentos...!
Abraços!
-
macburn
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Nov 02, 2010 14:36
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por MarceloFantini » Qua Nov 03, 2010 20:09
por MarceloFantini » Qua Nov 03, 2010 20:09
Qualquer livro de cálculo multivariável serve (desde que você saiba as regras de derivação de uma variável). Existe o Guidorizzi, Stewart, Boulos, Marilia Flemming, George Thomas...
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por macburn » Qua Nov 03, 2010 21:14
por macburn » Qua Nov 03, 2010 21:14
Boa noite Fantini,
Sem querer abusar meu nobre, será que você poderia descrever o passo-a-passo desta questão?
Meus agradecimentos!
-
macburn
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Nov 02, 2010 14:36
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por MarceloFantini » Qua Nov 03, 2010 21:31
por MarceloFantini » Qua Nov 03, 2010 21:31
Do cálculo de uma variável, para derivar o quociente de duas funções:
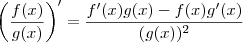
Quando temos funções de duas ou mais variáveis, o processo é similar, porém derivamos em relação à uma variável e mantemos as outras constantes, no caso feito,
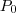
e

são outras variáveis, porém na hora de derivar foram mantidas constantes. Assim, na hora de derivar você enxerga a função deste modo:

E aplica como se fosse o cálculo de uma variável.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por macburn » Qua Nov 03, 2010 21:39
por macburn » Qua Nov 03, 2010 21:39
Boa noite Fantini,
Muito bom meu nobre! Foi bem esclarecedor sua explicação! Gostei muito. Que Deus continue iluminando sua mente. Parabéns!
Abraços!
-
macburn
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Nov 02, 2010 14:36
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por macburn » Dom Nov 07, 2010 13:00
por macburn » Dom Nov 07, 2010 13:00
Alô pessoal,
Boa tarde! Estou travando nessa essa equação para obter a derivada:
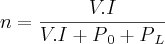
Lembrando que:
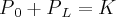
, então,
Utilizando a expressão:

Pessoal, travei aqui!

Se algum colega puder me mostrar como avançar,
desde já, meus sinceros agradecimentos...
-
macburn
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Nov 02, 2010 14:36
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por macburn » Seg Nov 08, 2010 21:15
por macburn » Seg Nov 08, 2010 21:15
Bom noite pessoal,
Como vai pessoal? Pessoal dei uma travada nessa derivada aí! Será que alguém quando dispuser de um tempo, por gentileza me dê uma força!
Abraços pessoal! Bons estudos a todos
-
macburn
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Nov 02, 2010 14:36
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por MarceloFantini » Seg Nov 08, 2010 22:06
por MarceloFantini » Seg Nov 08, 2010 22:06
A função

no caso é

e não

. Refaça usando isso.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por macburn » Ter Nov 09, 2010 21:02
por macburn » Ter Nov 09, 2010 21:02
Olá pessoal,
Grande Fantini, como vai meu brother. Sem qquerer abusar meu nobre, não teria como vc quebrar essa pra mim, até dar uma relembrada. Vou na biblioteca pegar um livro de calculo I para dar uma recordada. Se puder, serei imensamente grato meu nobre!
Abraços meu querido!
-
macburn
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Nov 02, 2010 14:36
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por macburn » Qua Nov 10, 2010 20:36
por macburn » Qua Nov 10, 2010 20:36
Boa noite pessoal,
Obrigado pela grande ajuda FAntini!
Um grande abraço meu nobre! Bons estudos...
-
macburn
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Nov 02, 2010 14:36
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Quero ver quem deriva essa!
por qrover » Qua Out 12, 2011 13:18
- 3 Respostas
- 2577 Exibições
- Última mensagem por wadson leite

Qui Out 13, 2011 13:52
Cálculo: Limites, Derivadas e Integrais
-
- Como resolver essa equação?
por viniciusantonio » Qua Out 21, 2009 19:17
- 1 Respostas
- 4148 Exibições
- Última mensagem por carlos r m oliveira

Qui Out 22, 2009 14:55
Cálculo: Limites, Derivadas e Integrais
-
- Como resolvo essa equação?
por LuizCarlos » Seg Jul 25, 2011 14:07
- 8 Respostas
- 4937 Exibições
- Última mensagem por LuizCarlos

Ter Jul 26, 2011 00:04
Sistemas de Equações
-
- Como expressar essa equação?
por Alerecife » Dom Nov 04, 2012 10:58
- 5 Respostas
- 2967 Exibições
- Última mensagem por Alerecife

Dom Abr 28, 2013 12:47
Funções
-
- Como resolver essa equação??
por lu1_cas2 » Ter Jul 29, 2014 02:50
- 1 Respostas
- 1466 Exibições
- Última mensagem por Russman

Sáb Ago 02, 2014 16:05
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
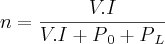


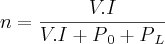







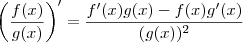
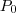 e
e  são outras variáveis, porém na hora de derivar foram mantidas constantes. Assim, na hora de derivar você enxerga a função deste modo:
são outras variáveis, porém na hora de derivar foram mantidas constantes. Assim, na hora de derivar você enxerga a função deste modo:



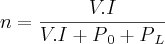
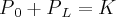 , então,
, então,







