Uns dias atrás estava tentando resolver essa questão de fundamental:
(EAM) Um cavalo deve ser amarrado a uma estaca situada em um dos vértices de um pasto que tem a forma de um quadrado, cujo lado mede 20m. Para que ele possa pastar em cerca de 20% da área total do pasto, a parte inteira, em metros, do comprimento da corda que o prende à estaca deve ser igual a:
A: 1 B:2 C:5 D:8 E:10
Eu estou absolutamente embolado nessa questão.
Um colega meu me explicou pela lógica, sem cálculo, e mesmo assim eu não entendi.
Eu tentei aqui agora calculando a diagonal dele. Um quadrado, lado 20, 20%=4. d=l.
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) => d=4.
=> d=4.![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) => 4.1,41=5,64.
=> 4.1,41=5,64.Só que, a resposta certa é 10.
Eu fui até onde eu consegui.
Ajudem!
Aloha!



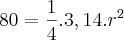
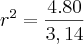




 .
.
 :
: