por Micael » Seg Mai 13, 2013 19:38
(CEFET-MG) Na figura ao lado, AB e CD são cordas de um circulo de centro O , que se cortam no ponto E. Se BÂC=30° e BÊC=85°,Então o angulo AôD mede: (OLHO SÓ PESSOAL, CONSEGUI ACHAR 120°) MAS NA QUESTÃO DIZ QUE A RESPOSTA É 110°) ALGUEM FAÇA ELA PRA EU VER.
- Anexos
-
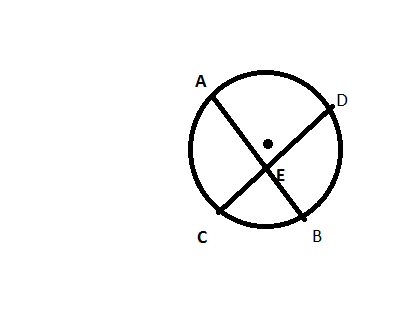
- geo.png (4.94 KiB) Exibido 2648 vezes
-
Micael
- Usuário Ativo
-
- Mensagens: 19
- Registrado em: Qui Jan 31, 2013 00:33
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
por Molina » Seg Mai 13, 2013 23:35
Boa noite,
Maciel.
Perceba o seguinte, que o fazendo AB, AC e CD formamos um triângulo ACE, onde temos que o ângulo A é igual a 30º. Neste triângulo, o ângulo E é suplementar ao ângulo BEC, ou seja, E = 95º. Como a soma dos ângulo internos do triângulo é 180º, o ângulo C do triângulo é 55º. Mas o ângulo C é o mesmo ângulo ACD (que é ângulo inscrito), e o ângulo AED é ângulo central. Logo, o ângulo central é o dobro do ângulo inscrito. Portanto, é igual a 110º.
Bom estudo
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-
Molina
- Colaborador Moderador - Professor
-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Duvida em geometria plana
por tadeutato » Seg Abr 25, 2011 11:26
- 2 Respostas
- 1580 Exibições
- Última mensagem por SidneySantos
Seg Abr 25, 2011 22:33
Geometria Plana
-
- Duvida - Geometria Plana
por Luiz Felipe » Ter Jun 05, 2012 21:32
- 2 Respostas
- 2730 Exibições
- Última mensagem por Pandaludo
Ter Ago 06, 2013 17:31
Geometria Plana
-
- Duvida - Geometria Plana 2
por Luiz Felipe » Ter Jun 05, 2012 22:27
- 1 Respostas
- 1065 Exibições
- Última mensagem por MarceloFantini
Qua Jun 06, 2012 02:38
Geometria Plana
-
- Duvida - Geometria Plana 3
por Luiz Felipe » Ter Jun 05, 2012 22:48
- 1 Respostas
- 7766 Exibições
- Última mensagem por MarceloFantini
Qua Jun 06, 2012 02:45
Geometria Plana
-
- [Geometria Plana] Duvida
por Micael » Qui Mar 14, 2013 17:57
- 1 Respostas
- 1041 Exibições
- Última mensagem por timoteo
Qui Mar 14, 2013 18:34
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de
Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é
Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:
Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:
Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
