 por raimundoocjr » Seg Jan 28, 2013 15:31
por raimundoocjr » Seg Jan 28, 2013 15:31
01. Qual o valor, em unidades de comprimento, que separa o baricentro do ponto A?

Respsota:
![2.\sqrt[]{2} 2.\sqrt[]{2}](/latexrender/pictures/ddf6c53cdaf7bbc107f4017b1175e22f.png)
Tive uma idéia de inciar com Geometria Analítica, colocando os eixos "x" e "y" iniciando do ponto A (vértice), mas a continuação não está tão clara ainda. Talvez estabelecendo retas, reta perpendicular e distância entre ponto e reta, eu consiga.
Já agradeço.
Editado pela última vez por raimundoocjr em Qua Jan 30, 2013 13:56, em um total de 1 vez.
-
raimundoocjr
-
 por sauloandrade » Seg Jan 28, 2013 18:24
por sauloandrade » Seg Jan 28, 2013 18:24
Eu fiz que nem você, começei por Geometria Analítica e continuei com os cálculos:

Se alguém souber fazer por geometria plana sem utilizar os conceitos de geometria analítica por favor poste a resolução por que fiquei curioso agora

-
sauloandrade
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Out 28, 2012 12:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Seg Jan 28, 2013 18:26
por Molina » Seg Jan 28, 2013 18:26
Boa tarde, Raimundo.
Seja
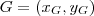
o baricentro do triângulo

. Utilize a formula para encontrar as coordenadas deste ponto:

e

Depois, prossiga como você estava pensando, colocando-o no plano cartesiano e faça a distância da origem até o ponto
G.
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por raimundoocjr » Seg Jan 28, 2013 18:40
por raimundoocjr » Seg Jan 28, 2013 18:40
Valeu Molina, fico grato. Mas, tenho curiosidade como o Saulo em saber como resolver apenas por Geometria Plana, se for possível é claro. Como proceder em exercícios assim, seria, talvez, mais fácil com duas visões distintas.

-
raimundoocjr
-
 por Molina » Seg Jan 28, 2013 19:27
por Molina » Seg Jan 28, 2013 19:27
Boa tarde.
raimundoocjr escreveu:Valeu Molina, fico grato. Mas, tenho curiosidade como o Saulo em saber como resolver apenas por Geometria Plana, se for possível é claro. Como proceder em exercícios assim, seria, talvez, mais fácil com duas visões distintas.

Seja H a altura deste triângulo isósceles. Temos a incrível propriedade que o baricentro G divide a altura em razões

e
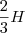
.
Ou seja, por Pitágoras descobrimos que a altura H do triângulo é 6. Desta forma, a distância do Baricentro ao ponto C é 4 e a distância do baricentro à base AB é 2. Formamos um novo triângulo retângulo de catetos 2 e hipotenusa X, que queremos descobrir.
Ficou mais fácil agora?

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por raimundoocjr » Seg Jan 28, 2013 19:38
por raimundoocjr » Seg Jan 28, 2013 19:38
Ficou sim. Eu me recordava sobre a propriedade, mas ela usava mais nos triângulos equiláteros. De qualquer forma esclareceu a resolução.

-
raimundoocjr
-
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria Plana] Triângulos isósceles
por DaviBahia » Sex Mar 22, 2013 13:23
- 2 Respostas
- 2876 Exibições
- Última mensagem por DaviBahia

Sáb Mar 23, 2013 06:16
Geometria Plana
-
- [Geometria Plana - Triângulo] Triângulo Isós. e Bissetriz
por raimundoocjr » Qua Fev 22, 2012 09:41
- 3 Respostas
- 6599 Exibições
- Última mensagem por DanielFerreira

Sáb Fev 25, 2012 01:37
Geometria Plana
-
- [Geometria Plana] Triângulo e Retas
por nerdbass » Qua Dez 28, 2016 18:08
- 0 Respostas
- 3134 Exibições
- Última mensagem por nerdbass

Qua Dez 28, 2016 18:08
Geometria Plana
-
- [Geometria Plana - Triângulo] Altura e Bissetriz
por raimundoocjr » Ter Fev 21, 2012 09:39
- 2 Respostas
- 2994 Exibições
- Última mensagem por Arkanus Darondra

Ter Fev 21, 2012 12:54
Geometria Plana
-
- Triângulo isósceles
por DanielFerreira » Qua Jul 29, 2009 16:03
- 3 Respostas
- 9675 Exibições
- Última mensagem por DanielFerreira

Qui Jul 30, 2009 17:35
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

![2.\sqrt[]{2} 2.\sqrt[]{2}](/latexrender/pictures/ddf6c53cdaf7bbc107f4017b1175e22f.png)




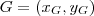 o baricentro do triângulo
o baricentro do triângulo  . Utilize a formula para encontrar as coordenadas deste ponto:
. Utilize a formula para encontrar as coordenadas deste ponto:



 e
e 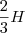 .
. 

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.