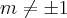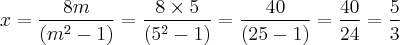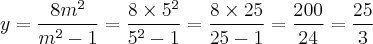por lsergio_santos » Qui Jun 11, 2015 17:12
por lsergio_santos » Qui Jun 11, 2015 17:12
Estou auxiliando minha filha com a matéria, mas devido ao longo tempo que me formei no 2º grau, não consigo me lembrar como desenvolver a solução para o problema a seguir:
Determine os valores de m para que as retas de equações y=mx-8 e y-x/m=0 sejam concorrentes. Alguém pode me ajudar a resolver passo a passo e, com urgência?
-
lsergio_santos
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Jun 11, 2015 17:03
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: marketing
- Andamento: formado
 por nakagumahissao » Qui Jun 11, 2015 19:04
por nakagumahissao » Qui Jun 11, 2015 19:04
lsergio_santos,
Boa tarde.
Para que as retas de equações y=mx-8 e y-x/m=0 sejam concorrentes deverá existir um ponto (x,y) iguais para as duas equações, ou seja:
Foi dado que:

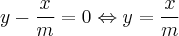
Assim, igualando as duas equações, tem-se:
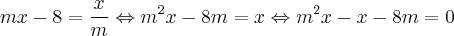
Isolando o x, teremos:
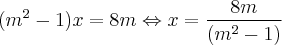
Usando quaisquer uma das equações dadas, podemos determinar o valor de y (usarei a primeira por ser mais simples):

Não sei se estão faltando dados no seu enunciado. Se for só isso mesmo, então quaisquer valores para m, com exceção de:


![m \neq \pm \sqrt[]{1} m \neq \pm \sqrt[]{1}](/latexrender/pictures/44fd1946f9828efa5bf57f4f0ee1532b.png)
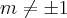
Ou seja, para valores de m onde o denominador se torna zero (m = 1 ou m = -1, conforme calculamos acima), encontraremos consequentemente os valores de x e y, onde as duas retas se coincidem.
Exemplo:
Tomemos m = 5 (pode ser qualquer valor diferente de 1 e -1):
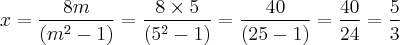
e
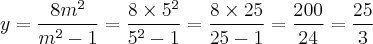
Ou seja:
Para m = 5, o ponto (5/3, 25/3) será o ponto onde as duas retas irão se encontrar e as equações das retas serão:
y = 5x - 8 e y - x/5 = 0, para este caso em particular.
Espero ter auxiliado.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Retas concorrentes
por marquinhoibvb » Qui Jun 05, 2008 22:39
- 1 Respostas
- 10654 Exibições
- Última mensagem por admin

Sex Jun 06, 2008 00:27
Geometria Analítica
-
- [GEOMETRIA ANALITICA] RETAS CONCORRENTES
por Patrick_GA » Qui Abr 23, 2015 10:52
- 0 Respostas
- 2136 Exibições
- Última mensagem por Patrick_GA

Qui Abr 23, 2015 10:52
Geometria Analítica
-
- Determinar se duas retas são concorrentes, paralelas...
por samra » Ter Mai 08, 2012 12:52
- 2 Respostas
- 5398 Exibições
- Última mensagem por samra

Ter Mai 08, 2012 22:23
Geometria Analítica
-
- [Geometria analítica] Duas retas concorrentes
por fernandocez » Qua Mai 08, 2013 18:48
- 3 Respostas
- 3897 Exibições
- Última mensagem por fernandocez

Sex Dez 20, 2013 09:54
Geometria Analítica
-
- Exercício sobre Feixe de retas concorrentes - DÚVIDA
por Danilo » Sáb Mai 26, 2012 21:00
- 6 Respostas
- 12875 Exibições
- Última mensagem por LuizAquino

Ter Out 14, 2014 13:43
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



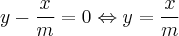
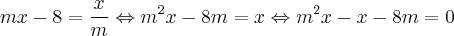
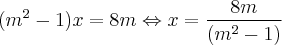



![m \neq \pm \sqrt[]{1} m \neq \pm \sqrt[]{1}](/latexrender/pictures/44fd1946f9828efa5bf57f4f0ee1532b.png)