 por Sohrab » Dom Jun 15, 2014 02:55
por Sohrab » Dom Jun 15, 2014 02:55
Amigos, estou com dificuldade em um problema que me parecia ser deveras simples.
Preciso calcular o terceiro lado de um triângulo, para encontrar seus ângulos internos que serão usados na decomposição vetorial de forças em um problema mecânico.
Desenhei o diagrama das medidas conhecidas e o valor que preciso (o x em vermelho).
Tentei por mais de uma hora e não consegui nada.. Alguém pode me dar uma força?

Obrigado!
-
Sohrab
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Qui Mar 18, 2010 17:42
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Téc. em Mec. Usinagem e Info Programação
- Andamento: cursando
 por e8group » Dom Jun 15, 2014 13:18
por e8group » Dom Jun 15, 2014 13:18
Como nem tudo que se vê é o que parece ser , faço uma pergunta : O diagrama representa um trapézio ?
Se sim ! Segue uma dica .
Considere o ABC o triangulo isósceles com
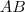
e

congruentes e base

e
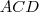
o triângulo de lados medindo
![\overline{AC} = x , \overline{AD} = 3 , \overline{AD}
Tome como verdade ( ou prove ) que [tex] \overline{AM} \overline{AC} = x , \overline{AD} = 3 , \overline{AD}
Tome como verdade ( ou prove ) que [tex] \overline{AM}](/latexrender/pictures/d6b1fb2aeb07389f9d09ec2804bf796d.png)
é a altura do trapézio . Em seguida , tome

a interseção da reta que contém a base maior do trapézio com à reta que passa por

e é paralela a reta que contém
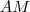
. Aceite (ou mostre) que
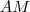
e
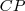
são congruentes e por conseguinte
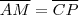
,segue-se que
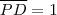
(Pq ?) .Como o triângulo PCD é T. retângulo , então pelo Teo. de Pitágoras ,
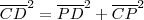
o que implica que
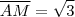
. Em seguida aplicando o Teo. de Pitágoras em
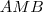
obterá

.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Como calcular lado de um Triângulo Escaleno?
por Lothor » Dom Jul 31, 2011 02:37
- 1 Respostas
- 2072 Exibições
- Última mensagem por giulioaltoe

Dom Jul 31, 2011 14:53
Trigonometria
-
- [Descobrir o terceiro ângulo do triângulo]
por Mayra Luna » Sex Dez 07, 2012 16:25
- 2 Respostas
- 1693 Exibições
- Última mensagem por Mayra Luna

Ter Dez 11, 2012 01:26
Trigonometria
-
- relação entre os lados de um triângulo
por geobson » Sáb Ago 17, 2013 15:28
- 0 Respostas
- 1200 Exibições
- Última mensagem por geobson

Sáb Ago 17, 2013 15:28
Geometria Plana
-
- Calcule os lados do triângulo retângulo
por andersontricordiano » Sex Mar 14, 2014 12:31
- 0 Respostas
- 1561 Exibições
- Última mensagem por andersontricordiano

Sex Mar 14, 2014 12:31
Trigonometria
-
- ÁREA DO TRIÂNGULO EM FUNÇÃO DOS LADOS
por Orlando Fagotti Neto » Qua Out 22, 2014 16:24
- 0 Respostas
- 1776 Exibições
- Última mensagem por Orlando Fagotti Neto

Qua Out 22, 2014 16:24
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



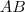 e
e  congruentes e base
congruentes e base  e
e 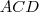 o triângulo de lados medindo
o triângulo de lados medindo ![\overline{AC} = x , \overline{AD} = 3 , \overline{AD}
Tome como verdade ( ou prove ) que [tex] \overline{AM} \overline{AC} = x , \overline{AD} = 3 , \overline{AD}
Tome como verdade ( ou prove ) que [tex] \overline{AM}](/latexrender/pictures/d6b1fb2aeb07389f9d09ec2804bf796d.png) é a altura do trapézio . Em seguida , tome
é a altura do trapézio . Em seguida , tome  a interseção da reta que contém a base maior do trapézio com à reta que passa por
a interseção da reta que contém a base maior do trapézio com à reta que passa por  e é paralela a reta que contém
e é paralela a reta que contém 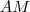 . Aceite (ou mostre) que
. Aceite (ou mostre) que 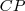 são congruentes e por conseguinte
são congruentes e por conseguinte 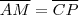 ,segue-se que
,segue-se que 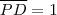 (Pq ?) .Como o triângulo PCD é T. retângulo , então pelo Teo. de Pitágoras ,
(Pq ?) .Como o triângulo PCD é T. retângulo , então pelo Teo. de Pitágoras , 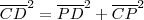 o que implica que
o que implica que 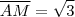 . Em seguida aplicando o Teo. de Pitágoras em
. Em seguida aplicando o Teo. de Pitágoras em  obterá
obterá  .
.