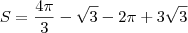Ressalvas feitas, vamos ao problema em questão.
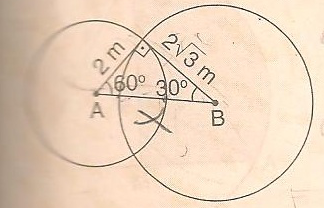
Recortei sua figura e anexei abaixo para o desenvolvimento da solução.
- geo0
- geo0.png (107.18 KiB) Exibido 1860 vezes
Obs: os valores apresentados abaixo saem por Área do Círculo, Pitágoras e Relações Trigonométricas nos triângulos analisados. Caso reste alguma dúvida sobre a obtenção dos valores retorne.
Se observar o círculo menor verá:
[A1] Um setor circular de raio 2 e ângulo central igual 120 graus ( 2 x 60 ) cuja área é igual

.
[A2] Um triângulo isósceles de lados iguais medindo

, base medindo
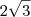
e altura igual a 1 , cuja área é igual a
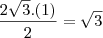
.
Se observar o círculo maior verá:
[A3] Um setor circular de raio
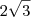
e ângulo central igual 60 graus ( 2 x 30 ) cuja área é igual
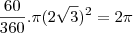
.
[A4] Um triângulo equilátero de lado medindo
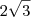
, base medindo
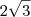
e altura igual a 3 , cuja área é igual a

.
A área solicitada é aquela compreendida pela intersecção dos dois círculos, então essa área vale:


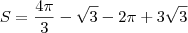
Substituindo os valores dados você chegará ao resultado.




 .
. , base medindo
, base medindo 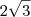 e altura igual a 1 , cuja área é igual a
e altura igual a 1 , cuja área é igual a 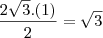 .
.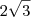 e ângulo central igual 60 graus ( 2 x 30 ) cuja área é igual
e ângulo central igual 60 graus ( 2 x 30 ) cuja área é igual 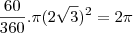 .
.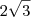 , base medindo
, base medindo 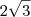 e altura igual a 3 , cuja área é igual a
e altura igual a 3 , cuja área é igual a  .
.