 a medida do lado do ctógono regular da figura. Então, a área da região sombreada é quanto?
a medida do lado do ctógono regular da figura. Então, a área da região sombreada é quanto?Sei que a área do octógono é :
 , supus que a parte sombreada é a metade da figira então é:
, supus que a parte sombreada é a metade da figira então é:  . Mas é apenas uma suposição, então como fazer?
. Mas é apenas uma suposição, então como fazer?
 a medida do lado do ctógono regular da figura. Então, a área da região sombreada é quanto?
a medida do lado do ctógono regular da figura. Então, a área da região sombreada é quanto? , supus que a parte sombreada é a metade da figira então é:
, supus que a parte sombreada é a metade da figira então é:  . Mas é apenas uma suposição, então como fazer?
. Mas é apenas uma suposição, então como fazer?


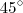 ?
?
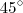 cada, de ângulo interno e que a base é
cada, de ângulo interno e que a base é 

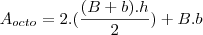
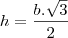
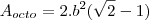

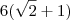 . Mas falta encontrar a área sombreada que depende da Base maior do trapézio ou o lado do retângulo. E agora, como faço?
. Mas falta encontrar a área sombreada que depende da Base maior do trapézio ou o lado do retângulo. E agora, como faço?
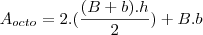
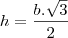
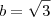



 , respectivamente.
, respectivamente. e portanto, os angulos da base maior dos trapezios medem
e portanto, os angulos da base maior dos trapezios medem 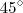 , ja que devem ser suplementares.
, ja que devem ser suplementares.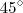 - hipotenusa eh o proprio lado do octógono- , temos que o triangulo tem lados iguais a
- hipotenusa eh o proprio lado do octógono- , temos que o triangulo tem lados iguais a 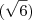 /2 ,
/2 , 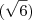 /2 e a
/2 e a 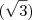 , este ultimo sendo o proprio lado do octogono.
, este ultimo sendo o proprio lado do octogono.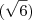 /2 e o outro medindo
/2 e o outro medindo 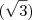 , paralelo ao proprio lado do octogono.
, paralelo ao proprio lado do octogono.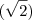 + 1.
+ 1. 
![\sqrt{3}\cdot\dfrac{3}{2}+2[\dfrac{(B+\sqrt{3})}{2}\cdot\dfrac{\sqrt{3}\cdot\sqrt{3}}{2}]=6(\sqrt{2}+1) \sqrt{3}\cdot\dfrac{3}{2}+2[\dfrac{(B+\sqrt{3})}{2}\cdot\dfrac{\sqrt{3}\cdot\sqrt{3}}{2}]=6(\sqrt{2}+1)](/latexrender/pictures/879fdffc19b29035f5b9b1a8dec690d2.png) e encontrei
e encontrei 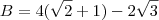 . Multiplicando isso bela base menor ja que a altura do retângulo é essa obti:
. Multiplicando isso bela base menor ja que a altura do retângulo é essa obti: 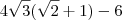 . Que não é o resultado. Eu não fiz certo? Posso ter errado nas contas?
. Que não é o resultado. Eu não fiz certo? Posso ter errado nas contas?

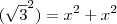

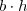


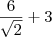
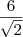 obtemos
obtemos 
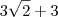







Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.