 por fernandocez » Qua Mar 16, 2011 13:47
por fernandocez » Qua Mar 16, 2011 13:47
Olá pessoal, eu consegui fazer toda questão mas a resposta não bate.
39) Em uma praia, dois observadoeres, A e B, estão distantes entre si 1000m. Ambos estão vendo uma pequena ilha C e, com seus instrumentos, medem os ângulos CÂB = 30° e CBA = 45°. Usando
![\sqrt[]{3}=1,73 \sqrt[]{3}=1,73](/latexrender/pictures/7dd46d8904d1e118c635a1442cee16b0.png)
, a distância aproximada de C até a reta AB é:
Eu fiz assim. Desenhei um triângulo, com angulo em A = 30° e em B = 45°, formou dois triângulos retângulos, com altura h (valor procurado).
tg 45 =

1 =

a = h
tg 30 =

=
![\frac{\sqrt[]{3}}{3} \frac{\sqrt[]{3}}{3}](/latexrender/pictures/80dc3f3832b00aa8da65bd3ac29edf6d.png)
=

=

=

1,73(1000 - a) = 3a
1730 - 1,73a = 3a
1730 = 3a +1,73a
4,73a = 1730
a =
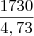
a = 365,8
A resposta encontrada é opção (d) 365 e a resposta pelo gabarito é (c) 355 m, qual resposta será que tá certa? Eu acho que fiz tudo certo. Aguardo uma ajuda dos feras.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por LuizAquino » Qua Mar 16, 2011 14:30
por LuizAquino » Qua Mar 16, 2011 14:30
39) Em uma praia, dois observadores, A e B, estão distantes entre si 1000m. Ambos estão vendo uma pequena ilha C e, com seus instrumentos, medem os ângulos

= 30° e
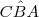
= 45°. Usando
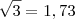
, a distância aproximada de C até a reta AB é:
A figura abaixo ilustra o exercício.

- triangulo-ABC.png (3.34 KiB) Exibido 2954 vezes
Usando a tangente de 30° podemos montar a equação

, de onde obtemos que
h é aproximadamente 365,8. Esta é a reposta correta.
Você deve verificar se o gabarito oficial não foi alterado. Vale lembrar que o gabarito oficial de um concurso só é alterado se algum candidato tiver entrado com recurso e este for deferido. Isso significa que pode ocorrer do gabarito oficial estar errado, mas ainda sim não ser corrigido, pois nenhum candidato apresentou um recurso válido.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Dvao » Qua Mar 16, 2011 23:10
por Dvao » Qua Mar 16, 2011 23:10
Concordo com a resposta de voces, ja fiz outros concursos ...
Em matematica é danado para alguma questao estar errada...
-
Dvao
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Mar 15, 2011 13:44
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Contabilidade
- Andamento: cursando
 por fernandocez » Qua Mar 16, 2011 23:36
por fernandocez » Qua Mar 16, 2011 23:36
Valeu pessoal.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão prova concurso (dúvida na resposta) 2
por fernandocez » Qua Mar 16, 2011 23:58
- 2 Respostas
- 1950 Exibições
- Última mensagem por fernandocez

Sex Mar 18, 2011 13:19
Álgebra Elementar
-
- Questão prova concurso (dúvida)
por fernandocez » Seg Mar 14, 2011 21:35
- 5 Respostas
- 2680 Exibições
- Última mensagem por fernandocez

Qua Mar 16, 2011 00:16
Logaritmos
-
- Questão prova concurso
por fernandocez » Sáb Fev 26, 2011 19:10
- 6 Respostas
- 3555 Exibições
- Última mensagem por fernandocez

Sáb Fev 26, 2011 22:29
Geometria Plana
-
- Questão prova concurso
por fernandocez » Sáb Fev 26, 2011 23:27
- 3 Respostas
- 2497 Exibições
- Última mensagem por fernandocez

Dom Fev 27, 2011 10:33
Funções
-
- Questão prova concurso (sen e cos)
por fernandocez » Qua Mar 02, 2011 11:26
- 13 Respostas
- 9279 Exibições
- Última mensagem por fernandocez

Dom Mar 13, 2011 12:18
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{3}=1,73 \sqrt[]{3}=1,73](/latexrender/pictures/7dd46d8904d1e118c635a1442cee16b0.png) , a distância aproximada de C até a reta AB é:
, a distância aproximada de C até a reta AB é:

 =
= ![\frac{\sqrt[]{3}}{3} \frac{\sqrt[]{3}}{3}](/latexrender/pictures/80dc3f3832b00aa8da65bd3ac29edf6d.png) =
=  =
=  =
= 
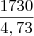


 = 30° e
= 30° e 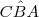 = 45°. Usando
= 45°. Usando  , a distância aproximada de C até a reta AB é:
, a distância aproximada de C até a reta AB é: , de onde obtemos que
, de onde obtemos que 
