Estou com dúvida em algumas questões de geometria. Poderia me dar umas dicas??
1. Qual a razão entre os comprimentos das circunferências circunscrita e inscrita a um quadrado?
sei que o lado do quadrado tem medida
![R\sqrt[]{2} R\sqrt[]{2}](/latexrender/pictures/b13c5d9de15baad3575f4c02037d38e5.png) e qua a apótema do quadrado é
e qua a apótema do quadrado é ![\frac{R\sqrt[]{2}}{2} \frac{R\sqrt[]{2}}{2}](/latexrender/pictures/32b3b9f53ac2cbb6adf26a539873f8db.png) e que esta é a mesma medida do raio da menor circunferência. É por aí?
e que esta é a mesma medida do raio da menor circunferência. É por aí?2. Se aumentarmos o comprimento de uma circunferência de 4cm, quanto aumentará o seu raio, em centímetros?
não sei por onde começar.


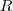 : raio da circunferência circunscrita
: raio da circunferência circunscrita : raio da circunferência inscrita
: raio da circunferência inscrita : comprimento da circunferência circunscrita
: comprimento da circunferência circunscrita : comprimento da circunferência inscrita
: comprimento da circunferência inscrita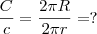

 : comprimento inicial da circunferência
: comprimento inicial da circunferência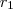 : raio inicial da circunferência
: raio inicial da circunferência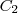 : comprimento final da circunferência
: comprimento final da circunferência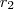 : raio final da circunferência
: raio final da circunferência

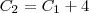

 R e que
R e que  . Cada medida de AP, AO, PO e OB tem o mesmo valor:r; então APOB = 3r. Se eu fizer
. Cada medida de AP, AO, PO e OB tem o mesmo valor:r; então APOB = 3r. Se eu fizer 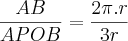 não daria a resposta: 1<x
não daria a resposta: 1<x
 . O que fiz errado?
. O que fiz errado? , mas não sei como relacioná-los ou achar o raio da menor.
, mas não sei como relacioná-los ou achar o raio da menor.

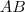 ?
?

 , pensando pela diferença das medidas.
, pensando pela diferença das medidas. ).
).

 , avisa que eu resolvo.
, avisa que eu resolvo.

