 por creberson » Qua Ago 08, 2012 16:32
por creberson » Qua Ago 08, 2012 16:32
ola boa ! tarde . estou prescisando de uma ajuda .
Prove que as faces laterais de uma piramide truncada regular são trapézios isósceles congruentes.
-
creberson
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Seg Jul 23, 2012 21:28
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: matematica
- Andamento: cursando
 por e8group » Qui Ago 09, 2012 11:07
por e8group » Qui Ago 09, 2012 11:07
Bom dia .
Em uma pirâmide regular temos uma região limitada pelo um polígono regular inscrito em uma circunferência ,esta região é área da base da pirâmide .Assim através de outro polígono regular ,onde seus lados são paralelos aos lados do polígono regular da pirâmide .Veja geometricamente ,em particular para um pentágono regular .
Pela figura em cada face da pirâmide regular nota-se que ,
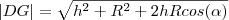
.Onde |DG| represanta uma aresta da face da pirâmide , de modo análogo para cada face da pirâmide chegaremos na mesma relação descrita acima oque implica que cada aresta da pirâmide regular são iguais .
Assim , concluímos que em cada face do tronco da pirâmide temos um trapézio isósceles onde suas bases são paralelas . Portanto em cada face temos traézios congruentes .
É isso .
Espero que ajude !
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por creberson » Qui Ago 09, 2012 21:25
por creberson » Qui Ago 09, 2012 21:25
ola boa noite.
não tem outra maneira mais simples de resolver ,esse exercicio?
-
creberson
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Seg Jul 23, 2012 21:28
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: matematica
- Andamento: cursando
 por e8group » Qui Ago 09, 2012 21:46
por e8group » Qui Ago 09, 2012 21:46
Eis a questão ,vou analisar .Mas a principio não vejo outra solução que seja mais simples ,evidentemente há outras ... mas não necessariamente uma solução implica menos trabalho que a outra .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- geometria espacial
por Gir » Seg Jul 27, 2009 11:46
- 3 Respostas
- 11733 Exibições
- Última mensagem por Molina

Ter Jul 28, 2009 15:21
Problemas do Cotidiano
-
- Geometria espacial
por nathy vieira » Qua Out 07, 2009 22:37
- 2 Respostas
- 2840 Exibições
- Última mensagem por nathy vieira

Qua Out 07, 2009 23:03
Geometria Espacial
-
- geometria espacial
por nathy vieira » Qua Out 07, 2009 23:18
- 4 Respostas
- 6138 Exibições
- Última mensagem por nathy vieira

Qui Out 08, 2009 18:37
Geometria Espacial
-
- Geometria espacial
por crixprof » Qui Out 15, 2009 10:40
- 2 Respostas
- 3152 Exibições
- Última mensagem por crixprof

Sex Out 16, 2009 18:27
Geometria Espacial
-
- Geometria Espacial
por geriane » Sáb Abr 03, 2010 10:39
- 4 Respostas
- 4196 Exibições
- Última mensagem por geriane

Dom Abr 04, 2010 10:29
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



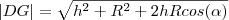 .Onde |DG| represanta uma aresta da face da pirâmide , de modo análogo para cada face da pirâmide chegaremos na mesma relação descrita acima oque implica que cada aresta da pirâmide regular são iguais .
.Onde |DG| represanta uma aresta da face da pirâmide , de modo análogo para cada face da pirâmide chegaremos na mesma relação descrita acima oque implica que cada aresta da pirâmide regular são iguais .




 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.