 por Alane » Qui Ago 02, 2012 09:45
por Alane » Qui Ago 02, 2012 09:45
Olá pessoal, gostaria muito da ajuda de vocês em uma questão da VUNESP. O enunciado diz o seguinte:
Uma escada tem 25 degraus iguais. A altura h de cada degrau está para a largura l assim como 2 está para 5. O desnível entre o quinto degrau e o pé da escada A é 1 metro. Qual a distância entre o pé da escada A e o topo da escada B?
Primeiramente tentei fazer uma semelhança de triângulos entre os primeiros 5 degraus com a altura 100 (por ser 1 metro) e um degrau de altura 2 e base 5. Com o resultado obtido que foi de 250 fiz o teorema de Pitágora para achar a hipotenusa. Achando está multipliquei por 25. O resultado deu um absurdo!! 135 metros entre A e B. Mas na verdade o resultado correto é 13m. Gostaria de saber o que fiz de errado e como chegar ao resultado correto!
Obrigada ^^
-
Alane
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Jul 05, 2012 22:42
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Russman » Qui Ago 02, 2012 10:42
por Russman » Qui Ago 02, 2012 10:42
A resposta é exatamente 13?
Nos meus cálculos eu encontro 12,9 m. Aproximando dá pra pensar em 13.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Russman » Qui Ago 02, 2012 10:53
por Russman » Qui Ago 02, 2012 10:53
Encontrei uma solução exata:
Nessa configuração a altura total da escada é
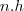
, onde

é o número de degraus e

a altura particular de cada um.
A distância entre o pé da escada e o todo do último degrau é dada por

, pois temos de descontar um degrau que não contribui!
Assim, seja

a distãncia do pé ao topo temos

Como exite a proporção

e o desnível do quinto degrau é um metro, isto é,
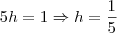
, então

.
Portanto,

.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Alane » Qui Ago 02, 2012 11:39
por Alane » Qui Ago 02, 2012 11:39
Nossa que olho de tandera!! kkkkkkkk
Muitissimooo obrigada, foi de muita utilidade sua ajuda!! ^^
-
Alane
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Jul 05, 2012 22:42
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- teorema de pitagoras
por stanley tiago » Sex Jan 21, 2011 15:59
- 5 Respostas
- 4666 Exibições
- Última mensagem por stanley tiago

Sáb Jan 22, 2011 15:49
Geometria Analítica
-
- teorema de pitagoras
por stanley tiago » Dom Fev 13, 2011 18:35
- 4 Respostas
- 3506 Exibições
- Última mensagem por stanley tiago

Seg Fev 14, 2011 22:00
Geometria Analítica
-
- teorema de pitagoras
por stanley tiago » Sáb Fev 19, 2011 10:26
- 1 Respostas
- 1924 Exibições
- Última mensagem por stanley tiago

Dom Fev 20, 2011 17:48
Geometria Analítica
-
- Teorema de Pitágoras
por Lorrane12 » Sex Mar 23, 2012 19:50
- 9 Respostas
- 12647 Exibições
- Última mensagem por DanielFerreira

Sex Mar 30, 2012 00:19
Trigonometria
-
- Teorema de Pitágoras
por Luciana Dias » Sex Mar 23, 2012 22:46
- 2 Respostas
- 1994 Exibições
- Última mensagem por Luciana Dias

Sex Mar 23, 2012 23:06
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



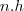 , onde
, onde  é o número de degraus e
é o número de degraus e  a altura particular de cada um.
a altura particular de cada um. , pois temos de descontar um degrau que não contribui!
, pois temos de descontar um degrau que não contribui! a distãncia do pé ao topo temos
a distãncia do pé ao topo temos
 e o desnível do quinto degrau é um metro, isto é,
e o desnível do quinto degrau é um metro, isto é, 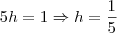 , então
, então  .
. .
.

 , avisa que eu resolvo.
, avisa que eu resolvo.

