Gstaria de saber como fica o valor das arestas da base
se formos calcular somente um pedaço da piramide, o tronco no caso
ele possivelmente dimiunui como eu encontro ?
por Aquamarine » Sáb Fev 11, 2012 16:15
por MarceloFantini » Sáb Fev 11, 2012 18:36
por Aquamarine » Sáb Fev 11, 2012 19:01
por MarceloFantini » Sáb Fev 11, 2012 21:00
, a razão entre os volumes será 
, logo a menor parte pesa menos de 10g. A maior parte pode ser obtida pegando a piramide toda e retirando a piramide acima, cujo volume está na razão 
do total, daí o volume estará na razão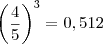 
, daí a maior parte tem peso 
kg ou 488 gramas. Portanto, a maior e a menor parte somam 496g e as três partes do meio somam juntas mais de 0,5kg.Voltar para Geometria Espacial
por solcruz » Sáb Mar 05, 2011 20:54
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)