Considere duas circunferências de raios iguais a R e centro em C1 e C2 , conforme a figura abaixo. Sabendo que a distância entre C1 e C2 é dada por 2s ( 0?s?R ) e que o ângulo A(C_2 ) ?B=?,
Considere duas circunferências de raios iguais a R e centro em C1 e C2 , conforme a figura abaixo. Sabendo que a distância entre C1 e C2 é dada por 2s ( 0?s?R ) e que o ângulo A(C_2 ) ?B=?,
a) Obtenha a expressão que fornece a área superposta
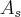
das duas circunferência em função de R,s e

[/quote]
A letra a, depois de muitas tentativas e por enquanto uma noite sem dormir fiz achando a área do setor circular menos a área do triangulo, esse resultado vezes dois:: ficou uma sopa de letrinhas, mas a intenção era essa!!! agora não estou conseguindo resolver o item b e c . Será que alguém pode me dar uma ajudinha???? Já teho a expressão do item a, mas não entendi como proceder nos itens seguintes!!!
b)Qual a posição relativa das circunferências quando A_s=0? Justifique utilizando a expressão obtida em a).
c)Qual a posição relativa das circunferências quando A_s=?R^2? Justifique utilizando a expressão obtida em a).
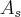 das duas circunferência em função de R,s e
das duas circunferência em função de R,s e


 (
(


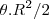
 e a área do triângulo Rs - s^2. Será :
e a área do triângulo Rs - s^2. Será : 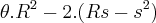 .
. em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.