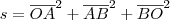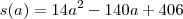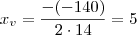por Danilo » Qui Mai 24, 2012 05:11
por Danilo » Qui Mai 24, 2012 05:11
Pessoal, estou com dificuldades para entender o enunciado... segue o exercício!
Entre os triângulos OAB com o vértice O na origem e os outros dois vértices A e B, respectivamente, nas retas y =1 e y =3 e alinhados com o ponto P(7,0), determine aquele para o qual é mínima a soma dos quadrados dos lados.
Mas por que ''os triângulos OAB''? ''determine aquele (seria aquele triangulo para o qual é mínima a soma dos quadrados dos lados?)
Quem puder me explicar e me dar idéia sobre qual caminho seguir eu agradeço!
Editado pela última vez por
Danilo em Sex Mai 25, 2012 03:30, em um total de 1 vez.
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Danilo » Qui Mai 24, 2012 05:30
por Danilo » Qui Mai 24, 2012 05:30
Bom, para tentar resolver, inicialmente, eu fiz o gráfico com o ponto (7,0), tracei respectivamente as retas que passam pelos pontos (0,1), (0,3), tracei também a reta que passa pelos pontos (0,1), (0,3), (7,0). Depois tracei um segmento que vai da origem até as retas... mas não consegui visualizar triângulo algum... . To meio confuso, quem puder dar uma luz aí.. agradeço!
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Sex Mai 25, 2012 11:32
por LuizAquino » Sex Mai 25, 2012 11:32
Danilo escreveu:Pessoal, estou com dificuldades para entender o enunciado... segue o exercício!
Entre os triângulos OAB com o vértice O na origem e os outros dois vértices A e B, respectivamente, nas retas y =1 e y =3 e alinhados com o ponto P(7,0), determine aquele para o qual é mínima a soma dos quadrados dos lados.
Mas por que ''os triângulos OAB''? ''determine aquele (seria aquele triangulo para o qual é mínima a soma dos quadrados dos lados?)
Quem puder me explicar e me dar idéia sobre qual caminho seguir eu agradeço!
Danilo escreveu:Bom, para tentar resolver, inicialmente, eu fiz o gráfico com o ponto (7,0), tracei respectivamente as retas que passam pelos pontos (0,1), (0,3), tracei também a reta que passa pelos pontos (0,1), (0,3), (7,0). Depois tracei um segmento que vai da origem até as retas... mas não consegui visualizar triângulo algum... . To meio confuso, quem puder dar uma luz aí.. agradeço!
As figuras abaixo ilustram três exemplos para o triângulo OAB. Mas note que há infinitos exemplos. Basta "deslizar" o ponto A sobre a reta y = 1 que teremos um outro ponto B correspondente na reta y = 3 (e de tal modo que A, B e P estão alinhados).
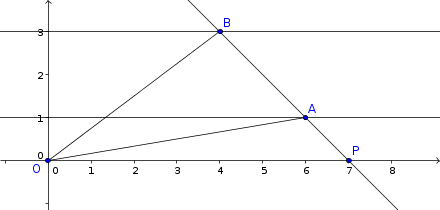
- figura1.png (4.39 KiB) Exibido 3922 vezes
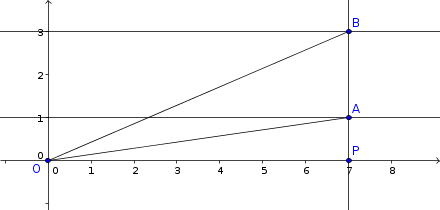
- figura2.png (4.25 KiB) Exibido 3922 vezes

- figura3.png (5.21 KiB) Exibido 3922 vezes
De todos os infinitos triângulos OAB que podemos formar, deseja-se aquele que tem a seguinte soma como a menor possível:
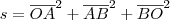
Agora tente concluir o execício. Se você não conseguir, então poste aqui até onde você conseguiu avançar.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Danilo » Sáb Mai 26, 2012 15:12
por Danilo » Sáb Mai 26, 2012 15:12
Bom, tentei fazer assim:
Chamei o ponto B (b,3), o ponto A (a, 1). Como B, A e P estão alinhados, peguei os 3 pontos, montei o determinante e igualei a zero. Coloquei b em função de a e vi que b = 3a - 14. Aí, fazendo a distância entre os pontos OB, OA E BA e elevando tudo ao quadrado, logo vou obter o quadrado dos lados + a distância. Aí, cheguei no polinomio de segundo grau 14a² - 140a + 406 e não consegui terminar. Está correto o racionio? Tem maneiras mais simples de resolver? Valeu!
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Sáb Mai 26, 2012 18:48
por LuizAquino » Sáb Mai 26, 2012 18:48
Danilo escreveu:Chamei o ponto B (b,3), o ponto A (a, 1). Como B, A e P estão alinhados, peguei os 3 pontos, montei o determinante e igualei a zero. Coloquei b em função de a e vi que b = 3a - 14. Aí, fazendo a distância entre os pontos OB, OA E BA e elevando tudo ao quadrado, logo vou obter o quadrado dos lados + a distância. Aí, cheguei no polinomio de segundo grau 14a² - 140a + 406 e não consegui terminar. Está correto o racionio?
Esse é o raciocínio esperado para o exercício.
Note que no final você obteve uma função como:
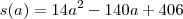
Se você fizesse o gráfico dessa função, então teria uma parábola com concavidade para cima. Sendo assim, o vértice dessa parábola é o ponto de mínimo dessa função. A coordenada x desse vértice será dada por:
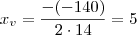
Temos então que para a = 5 a soma será a menor possível.
Lembrando agora que b = 3a - 14, temos que b = 1.
Portanto, os pontos são A = (5, 1) e B = (1, 3).
Danilo escreveu:Tem maneiras mais simples de resolver?
Eu acredito que essa já é a maneira mais simples.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Danilo » Sáb Mai 26, 2012 18:59
por Danilo » Sáb Mai 26, 2012 18:59
A é mesmo... pela enésima vez, muito obrigado !
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Exercício sobre equação da reta - Dúvida
 por Danilo » Seg Mai 07, 2012 00:28
por Danilo » Seg Mai 07, 2012 00:28
- 2 Respostas
- 1942 Exibições
- Última mensagem por Danilo

Dom Mai 13, 2012 22:38
Geometria Analítica
-
- Dúvida em exercício sobre equação da reta
por Danilo » Dom Mai 13, 2012 22:05
- 6 Respostas
- 3389 Exibições
- Última mensagem por Danilo

Qua Mai 16, 2012 01:19
Geometria Analítica
-
- Duvida em exercício {equação da reta/perpendicularismo}
por Danilo » Qui Jun 14, 2012 06:15
- 2 Respostas
- 1840 Exibições
- Última mensagem por Danilo

Sáb Jun 16, 2012 03:22
Geometria Analítica
-
- interseção,área e reta dúvida exercício
por igor44 » Seg Out 31, 2011 21:20
- 1 Respostas
- 2127 Exibições
- Última mensagem por procyon

Ter Nov 01, 2011 00:57
Geometria Analítica
-
- [Ângulo - reta e plano] Dúvida exercício
por MrJuniorFerr » Sex Out 12, 2012 11:51
- 6 Respostas
- 4613 Exibições
- Última mensagem por MarceloFantini

Sex Out 12, 2012 20:18
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.