felipeke escreveu:Os coeficientes angular e linear da reta 3y-2x=12=0 é?
Eu presumo que a equação da reta seja:
3y - 2x - 12 = 0
Note que você escreveu dois símbolos de "=" no seu texto.
Pois bem, suponha que você tem uma reta no formato:
ax + by + c = 0
Isolando a variável y, você pode colocá-la no seguinte formato:

O coeficiente
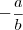
será o angular. Já o coeficiente
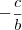
será o linear.
Agora isole a variável y na equação dada no exercício. Em seguida, basta identificar os coeficientes.
felipeke escreveu:O triângulo de verticies A(4,3) , B (6,-2) e C (-11,-3) é? Prove.
"É" o que? Está faltando algum texto. Não seria algo como segue abaixo?
"
O triângulo de vértices A(4,3), B (6,-2) e C (-11,-3) é retângulo? Prove."
Se esse for o caso, então siga os seguintes passos:
1) A reta que passa por AB é perpendicular a reta que passa por AC? Caso seja, então é triângulo retângulo e você pode parar nesse passo. Caso contrário, vá para o próximo passo.
2) A reta que passa por BA é perpendicular a reta que passa por BC? Caso seja, então é triângulo retângulo e você pode parar nesse passo. Caso contrário, vá para o próximo passo.
3) A reta que passa por CA é perpendicular a reta que passa por CB? Caso seja, então é triângulo retângulo e você pode parar nesse passo. Caso contrário, como em todos os passos a resposta foi não, temos que não se trata de um triângulo retângulo.
 Ola pessoal, não estou conseguido resolver estas continha ,principalmente a do triangulo lá vai elas:
Ola pessoal, não estou conseguido resolver estas continha ,principalmente a do triangulo lá vai elas:
 Ola pessoal, não estou conseguido resolver estas continha ,principalmente a do triangulo lá vai elas:
Ola pessoal, não estou conseguido resolver estas continha ,principalmente a do triangulo lá vai elas:

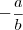 será o angular. Já o coeficiente
será o angular. Já o coeficiente 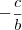 será o linear.
será o linear.


 , avisa que eu resolvo.
, avisa que eu resolvo.

