O problema é o seguinte tem um Trinagulo com os lados todos iguais AB =BC=CA 2 cm!
A figura esta com o AB como base e traçou-se ou recta paralela a um dos lados BC que deu origem a duas figuras com a mesma área!
Uma delas é um triangulo igual mas mais pequeno e outra um "trapezio"! Pede para calcular o tamanho da recta paralela!
Ora bem, eu calculei a altura do triangulo que é igual
 +
+  =
= 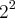 => b =
=> b =![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png)
Calculando a área temos
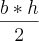 =
= ![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png) e agora?
e agora?Se as duas figuras têm a mesma area significa que cada uma vai ter metade de
![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png) , mas pela formula do triangulo temos que
, mas pela formula do triangulo temos que ![\frac{b*h}{2}=\frac{\sqrt[]{3}}{2} \frac{b*h}{2}=\frac{\sqrt[]{3}}{2}](/latexrender/pictures/b2a9b7575c3baafa4938ffdb30cdd412.png) o que nos dá duas incógnitas :S
o que nos dá duas incógnitas :SComo fazer? Esta no capitulo de razão de semelhança, tenho de usar aqui? como?
Obrigado


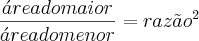 e depois é so substituir uma vez a a área do maior será
e depois é so substituir uma vez a a área do maior será ![\frac{\sqrt[]{3}}{2} \frac{\sqrt[]{3}}{2}](/latexrender/pictures/21682d7c1e802e9b52a99c01850489c4.png) .
.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)