Alguém poderia me ajudar a fazer o seguinte exercício?
a)Mostre que v=(a,b) e w(-b,a) são vetores ortogonais;
b) Use o resultado da parte (a) para encontrar dois vetores ortogonais a v=(2,-3);
c) encontre dois vetores unitários que são ortogonais a (-3,4)




 .
. um vetor procurado.
um vetor procurado.  .
. . Logo,
. Logo,  .
.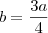 e substituindo em
e substituindo em 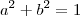 temos:
temos: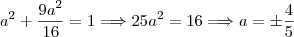
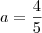 temos
temos  .
.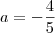 temos
temos  .
.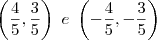 .
.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)