 por rogeriobautz » Qui Abr 01, 2010 01:56
por rogeriobautz » Qui Abr 01, 2010 01:56
Olá pessoal, eu preciso saber como resolver o seguinte exercicio:
Conhecendo-se u = (1 , 2, 0 ), v = (0, 1, 3) e w = (-1, 3, 1) calcular
os escalares m, n e p em mu + nv + pw = (0, 0, 14).
(Onde u, v e w são vetores)(A resposta é m = -1, n = 5, p = -1)
Já tentei separar as sentenças para calcular, tipo:
m.1+n.0+p.(-1)=0
m.2+n.1+p.3=0
m.0+n.3+p.1=14
mas não consegui chegar na resposta correta.
Preciso de ajuda, pois tenho prova amanhã(01/04/09) e ira ter questões similares.
Eu entrei na facul com 2 meses de atraso por isso estou na correria.
-
rogeriobautz
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Abr 01, 2010 01:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecatrônica
- Andamento: cursando
 por MarceloFantini » Qui Abr 01, 2010 03:15
por MarceloFantini » Qui Abr 01, 2010 03:15
Boa noite.
Pelo sistema que você montou, na primeira equação é trivial que

. Logo, segue que

e
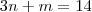
. Resolvendo, encontramos que

, portanto
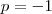
e

. Você apenas parou no meio, se tivesse resolvido o sistema teria chegado na resposta. Não tenha medo de tentar!
Espero ter ajudado.
Um abraço.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calcular det(A-x.I)
por Bruhh » Sáb Jun 05, 2010 18:59
- 3 Respostas
- 4487 Exibições
- Última mensagem por MarceloFantini

Seg Jun 07, 2010 12:26
Matrizes e Determinantes
-
- (ITA) Calcular x + y
por Carolziiinhaaah » Qui Jun 24, 2010 14:47
- 3 Respostas
- 2644 Exibições
- Última mensagem por DanielFerreira

Ter Jun 29, 2010 16:37
Matrizes e Determinantes
-
- calcular:
por willwgo » Qui Mai 05, 2011 16:33
- 1 Respostas
- 1637 Exibições
- Última mensagem por FilipeCaceres

Qui Mai 05, 2011 19:51
Polinômios
-
- Calcular a.b
por -civil- » Ter Set 20, 2011 23:29
- 3 Respostas
- 2626 Exibições
- Última mensagem por MarceloFantini

Qui Set 29, 2011 21:07
Polinômios
-
- (Calcular)
por Veronica Souza » Ter Abr 24, 2012 13:06
- 6 Respostas
- 4319 Exibições
- Última mensagem por Fabiano Vieira

Seg Mai 28, 2012 23:30
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 . Logo, segue que
. Logo, segue que  e
e 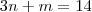 . Resolvendo, encontramos que
. Resolvendo, encontramos que  , portanto
, portanto  e
e  . Você apenas parou no meio, se tivesse resolvido o sistema teria chegado na resposta. Não tenha medo de tentar!
. Você apenas parou no meio, se tivesse resolvido o sistema teria chegado na resposta. Não tenha medo de tentar!
