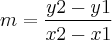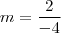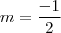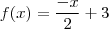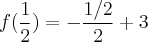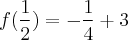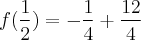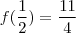por Neydimara » Ter Ago 05, 2014 19:27
por Neydimara » Ter Ago 05, 2014 19:27
O grafico da funçao f é o segmento de reta que une os pontos (22,2) e (2,0). O valor de f (1/2) é:
a) 1 b) 3/4 c)1/2 d) 1/8 e)7/8
A resposta dessa questã é a letra B, eu sei que é essa resposta mas não sei como realizar a equaçao que a define. Tente pelo y2-y1/x2-x1 e não consegui, então pesquisei e vi que no lugar de (22,2) é (-2,2), tentei do mesmo jeito e não consegui, me ajudem preciso da justificativa :'(
-
Neydimara
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Ago 05, 2014 19:13
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por jcmatematica » Sex Set 26, 2014 18:05
por jcmatematica » Sex Set 26, 2014 18:05
Neydimara escreveu:O grafico da funçao f é o segmento de reta que une os pontos (22,2) e (2,0). O valor de f (1/2) é:
a) 1 b) 3/4 c)1/2 d) 1/8 e)7/8
A resposta dessa questã é a letra B, eu sei que é essa resposta mas não sei como realizar a equaçao que a define. Tente pelo y2-y1/x2-x1 e não consegui, então pesquisei e vi que no lugar de (22,2) é (-2,2), tentei do mesmo jeito e não consegui, me ajudem preciso da justificativa :'(
A equação da reta é da forma ax + b
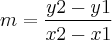

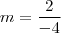
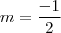
Nosso coeficiente angular é -1/2. Então temos que f(x) = -x/2 + b
Vamos decobrir o valor de b.
f(2) = 2
-2/2 + b = 2
b = 2 + 1
b = 3
b = 3Agora conhecemos a equação da reta
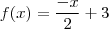
O exercício pede para calcularmos f(1/2)
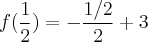
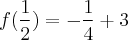
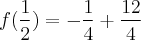
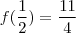
-
jcmatematica
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Ter Jul 29, 2014 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em matematica
- Andamento: formado
 por DanielFerreira » Sex Set 26, 2014 23:52
por DanielFerreira » Sex Set 26, 2014 23:52
JC, não compreendi os pontos que aplicou na fórmula para encontrar o coeficiente angular.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por jcmatematica » Sáb Set 27, 2014 15:24
por jcmatematica » Sáb Set 27, 2014 15:24
danjr5 escreveu:JC, não compreendi os pontos que aplicou na fórmula para encontrar o coeficiente angular.
A Neydimara disse que os pontos são (22, 2) e (2, 0).
Porém, logo abaixo, ela disse que os pontos corretos são (-2, 2) e (2, 0).
Então usei estes pontos
(-2, 2) e (2, 0)
-
jcmatematica
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Ter Jul 29, 2014 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em matematica
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Retas e pontos
por Neydimara » Ter Ago 05, 2014 19:21
- 1 Respostas
- 1056 Exibições
- Última mensagem por Cleyson007

Qua Ago 06, 2014 21:14
Geometria Analítica
-
- [Retas] Pontos equidistantes
por luankaique » Qui Jul 25, 2013 22:34
- 2 Respostas
- 2118 Exibições
- Última mensagem por luankaique

Sex Jul 26, 2013 14:11
Geometria Analítica
-
- Relação entre cordas entre dois pontos de retas.
por janderson77 » Seg Dez 02, 2013 12:00
- 0 Respostas
- 2057 Exibições
- Última mensagem por janderson77

Seg Dez 02, 2013 12:00
Trigonometria
-
- [RETAS] Descobrir ponto através de retas
 por renan_a » Qui Set 27, 2012 11:10
por renan_a » Qui Set 27, 2012 11:10
- 5 Respostas
- 3084 Exibições
- Última mensagem por renan_a

Sáb Set 29, 2012 18:37
Geometria Analítica
-
- [Pontos críticos - Derivadas] Ajuda com pontos críticos
por jonaskessinger » Qui Dez 13, 2012 18:16
- 1 Respostas
- 3583 Exibições
- Última mensagem por Russman

Qui Dez 13, 2012 19:35
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.