 por engel » Qua Dez 30, 2009 17:03
por engel » Qua Dez 30, 2009 17:03
Tenho uma questão da FUVEST que diz assim:
A reta s passa pelo ponto (0,3) e é perpendicular à reta AB onde A=(0,0), e B é o centro da circinferência x²+y²-2x-4y=20. Então a equação de s é:
a)x-2y=-6
b) x+2y=6
c) x+y=3
d) y-x=3
e) 2x+y=6
A única forma de encontrar a resposta foi assim: y-yp=m.x-xp
y-3=-1/2.x-0
y-3=-x/2
x+2y=6 (B)
Mas pq ñão consigo achar resposta usando a fórmula do Raio da circinfeRência ( R= (raiz de Xc²+yc²-F) e então usar: (x-xc)²+(y+yc)²=R². Com esta fórmula não obterei a equação da reta?
Obrigada!
-
engel
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Dez 30, 2009 16:38
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Qui Dez 31, 2009 15:55
por MarceloFantini » Qui Dez 31, 2009 15:55
Boa tarde Engel!
Acredito que você tenha errado a resposta e vou mostrar o porque.
Primeiro, fiz uma figura para que você veja a situação (caso você não tenha feito):

Para começar o problema, devemos calcular o coeficiente angular de AB:
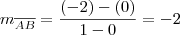
Como a reta

é perpendicular à reta

, temos:


Tendo o coeficiente angular e um ponto, podemos encontrar a equação da reta usando
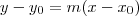
:

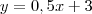
Multiplicando ambos lados por 2:
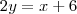
Trocando de lado 6 e 2y:

Que é a resposta
A.
Espero ter ajudado!
Um abraço e Feliz Ano Novo!
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Outra Dúvida
por rodsales » Sáb Jun 06, 2009 21:41
- 1 Respostas
- 1495 Exibições
- Última mensagem por Marcampucio

Sáb Jun 06, 2009 22:38
Trigonometria
-
- Outra dúvida
por rodsales » Qui Jun 18, 2009 22:12
- 1 Respostas
- 1432 Exibições
- Última mensagem por Marcampucio

Sex Jun 19, 2009 00:48
Trigonometria
-
- Outra dúvida.
por rodsales » Seg Out 12, 2009 09:56
- 1 Respostas
- 1507 Exibições
- Última mensagem por Marcampucio

Seg Out 12, 2009 11:59
Trigonometria
-
- Outra duvida
por GABRIELA » Qui Fev 11, 2010 17:57
- 1 Respostas
- 1719 Exibições
- Última mensagem por MarceloFantini

Sex Fev 12, 2010 01:05
Geometria Espacial
-
- Outra Dúvida - Conjuntos
por joaopedrel » Dom Mar 14, 2010 20:03
- 2 Respostas
- 1672 Exibições
- Última mensagem por joaopedrel

Dom Mar 14, 2010 22:57
Conjuntos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



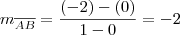
 é perpendicular à reta
é perpendicular à reta  , temos:
, temos:

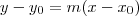 :
:
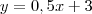
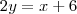



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.