 por rochadapesada » Dom Dez 15, 2013 16:31
por rochadapesada » Dom Dez 15, 2013 16:31
Não consigo desenrolar essa questão... PS.: como não dei algebra linear, então por favor não usem
- Anexos
-

-
rochadapesada
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Abr 04, 2013 22:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por e8group » Dom Dez 15, 2013 16:40
por e8group » Dom Dez 15, 2013 16:40
O que você não entendeu ? Outra forma de escrever o enunciado .Dado a reta

e os pontos

.Encontre um ponto pertencendo à reta

tal que a distância deste ponto ao ponto

seja a mesma ao ponto

. Em resumo , deve determinar

.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por rochadapesada » Dom Dez 15, 2013 17:24
por rochadapesada » Dom Dez 15, 2013 17:24
Sim, mas, iria ficar o seguinte neh:
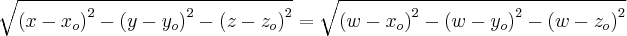
ai fazendo as contas acho x0 + y0= 2, mas depois? O que faço?
-
rochadapesada
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Abr 04, 2013 22:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por e8group » Dom Dez 15, 2013 18:04
por e8group » Dom Dez 15, 2013 18:04
Na verdade a distância entre dois pontos
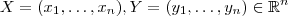
e dada por
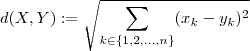
. Por exemplo em

.
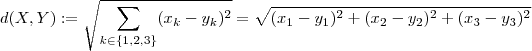
e não a fórmula que você apresentou .
Note que se
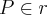
então para algum

real ,tem-se
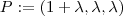
. Em particular devemos escolher

tal que
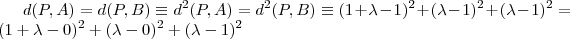
.
Tente avançar .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por rochadapesada » Dom Dez 15, 2013 18:18
por rochadapesada » Dom Dez 15, 2013 18:18
Eu ainda não vi isso amigo... Como vou fazer um negócio que o livro nem mostra essa sua explicação :/
-
rochadapesada
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Abr 04, 2013 22:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por e8group » Dom Dez 15, 2013 18:41
por e8group » Dom Dez 15, 2013 18:41
O livro fala sobre produto escalar ou interno,pois conheço tal livro .Então ,
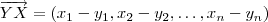
. Calculando o produto escalar

em termos das componentes destes vetores vamos obter
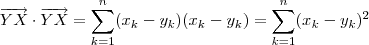
. A raiz quadrada desta expressão forne a distância de

a

.
Agora como queres obter um ponto P equidistante de A,B sem impor que as distância dele a ambos pontos são iguais ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por rochadapesada » Dom Dez 15, 2013 19:04
por rochadapesada » Dom Dez 15, 2013 19:04
Mas pode ter x-y? Porque eles são eixos diferentes (uma é abscissa e a outra é ordenada) e nesse livro aprendi que tem que somar ou subtrair apenas pelo seu respectivo eixo... Essa parte não consta no livro :/
-
rochadapesada
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Abr 04, 2013 22:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Russman » Dom Dez 15, 2013 19:55
por Russman » Dom Dez 15, 2013 19:55
A notação só está complicada. Eu penso ser melhor escrever os vetores de uma forma diferente.
Como calcular a distância entre uma reta

e um ponto

?
Dados dois pontos
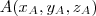
e
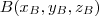
o vetor que liga estes pontos é escrito como

e suas componentes são as diferenças das coordenadas respectivas de cada ponto. Isto é,

.
Você sabe que os pontos
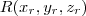
da reta

são todos escritos da forma



.
Assim, o vetor que liga a reta

ao ponto

é

e ao ponto
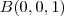
é

Pronto. Agora a distância entre a reta e o ponto será o módulo do respectivo vetor de ligação.
Se você deseja que as distâncias sejam iguais basta igualar os módulos. Assim, você obterá uma equação em

e , com a solução, poderá calcular o respectivo ponto da reta que dista o mesmo de

e

.
Eu acho que vai ser o ponto

a solução.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por rochadapesada » Dom Dez 15, 2013 21:14
por rochadapesada » Dom Dez 15, 2013 21:14
agora entendi, vlw =DD
-
rochadapesada
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Abr 04, 2013 22:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- geometria analítica estudo da reta ponto de interseção
por jeffersonricardo » Dom Ago 22, 2010 08:27
- 0 Respostas
- 1507 Exibições
- Última mensagem por jeffersonricardo

Dom Ago 22, 2010 08:27
Geometria Analítica
-
- geometria analítica estudo da reta ponto de interseção
por jeffersonricardo » Dom Ago 22, 2010 08:27
- 0 Respostas
- 1374 Exibições
- Última mensagem por jeffersonricardo

Dom Ago 22, 2010 08:27
Geometria Analítica
-
- geometria analítica estudo da reta distancia do ponta à reta
por jeffersonricardo » Dom Ago 22, 2010 08:29
- 1 Respostas
- 2408 Exibições
- Última mensagem por Pedro123

Seg Ago 23, 2010 22:24
Geometria Analítica
-
- [GA - Estudo da Reta] Exercício de GA com reta e plano
por matheus0807 » Qui Jun 05, 2014 15:12
- 0 Respostas
- 2104 Exibições
- Última mensagem por matheus0807

Qui Jun 05, 2014 15:12
Geometria Analítica
-
- [Estudo da reta] Determinar a equação de uma reta
por Isabelagarcia » Qui Jul 24, 2014 23:45
- 0 Respostas
- 1588 Exibições
- Última mensagem por Isabelagarcia

Qui Jul 24, 2014 23:45
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 e os pontos
e os pontos  .Encontre um ponto pertencendo à reta
.Encontre um ponto pertencendo à reta  tal que a distância deste ponto ao ponto
tal que a distância deste ponto ao ponto  seja a mesma ao ponto
seja a mesma ao ponto . Em resumo , deve determinar
. Em resumo , deve determinar  .
.
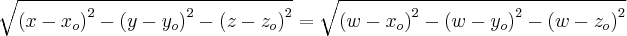

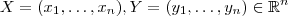 e dada por
e dada por 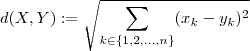 . Por exemplo em
. Por exemplo em  .
. 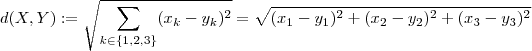 e não a fórmula que você apresentou .
e não a fórmula que você apresentou . 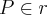 então para algum
então para algum  real ,tem-se
real ,tem-se 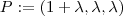 . Em particular devemos escolher
. Em particular devemos escolher  tal que
tal que 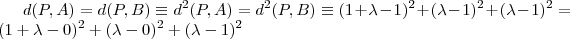 .
. 

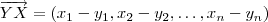 . Calculando o produto escalar
. Calculando o produto escalar  em termos das componentes destes vetores vamos obter
em termos das componentes destes vetores vamos obter 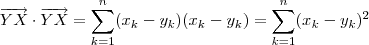 . A raiz quadrada desta expressão forne a distância de
. A raiz quadrada desta expressão forne a distância de  a
a  .
. 

 e um ponto
e um ponto  ?
? 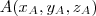 e
e 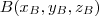 o vetor que liga estes pontos é escrito como
o vetor que liga estes pontos é escrito como  e suas componentes são as diferenças das coordenadas respectivas de cada ponto. Isto é,
e suas componentes são as diferenças das coordenadas respectivas de cada ponto. Isto é,  .
. 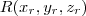 da reta
da reta  são todos escritos da forma
são todos escritos da forma 

 .
. ao ponto
ao ponto  é
é
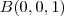 é
é
 e , com a solução, poderá calcular o respectivo ponto da reta que dista o mesmo de
e , com a solução, poderá calcular o respectivo ponto da reta que dista o mesmo de  e
e  .
. a solução.
a solução.



 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.