Um quadrado ABCD tem a diagonal BD contida na reta r: x=1 ;y=z . Sabendo que A(0,0,0), determine os vértices B,C e D.
Valew.
por mih123 » Seg Abr 01, 2013 21:01
por e8group » Ter Abr 02, 2013 01:31
(interseção dos planos 
e 
)dada ,por sua configuração ,obtemos que se o segmento 
(que é a diagonal do quadrado ) está contido em temos que a tripla-ordenadas dos pontos 
e 
é solução da equação da reta .Podemos tomar 
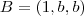e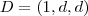 
para algum 
e 
reais tais que seja a diagonal do quadrado .
,basta ver que os vetores 
e 
possuem a mesma direção (são paralelos) ,norma (comprimento) e o mesmo sentido ,isto é ,eles são iguais .Sendo assim ,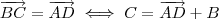 
.Como foi dado que 
temos que 
.
Voltar para Geometria Analítica
por rochadapesada » Dom Dez 15, 2013 16:31
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)