 por Danilo » Sex Out 26, 2012 01:15
por Danilo » Sex Out 26, 2012 01:15
Dadas as retas
r:
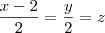
e s: x-2 = y = z, obtenha uma equação geral para o plano determinado por r e s.
Bom, sei como encontrar a equação do plano obtendo a normal e um de seus pontos mas eu não vejo como fazer isso tendo duas retas. E não vejo como duas retas determinam um plano... Grato desde já!
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Sex Out 26, 2012 02:37
por MarceloFantini » Sex Out 26, 2012 02:37
Seja

o parâmetro da primeira reta e
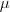
da segunda.
Então
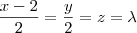
e

.
Daí,

e

Na notação usual, a reta

será dada por

e a reta

por
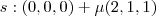
.
Para obter a equação geral, faça como no
outro tópico: calcule o produto vetorial dos vetores diretores, ou seja, calcule

e substitua
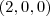
para encontrar o coeficiente que falta.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Danilo » Sex Out 26, 2012 10:31
por Danilo » Sex Out 26, 2012 10:31
MarceloFantini escreveu:Seja

o parâmetro da primeira reta e
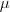
da segunda.
Então
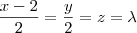
e

.
Daí,

e

Na notação usual, a reta

será dada por

e a reta

por
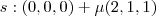
.
Para obter a equação geral, faça como no
outro tópico: calcule o produto vetorial dos vetores diretores, ou seja, calcule

e substitua
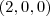
para encontrar o coeficiente que falta.
Mais uma vez, obrigado Marcelo! Entendi!
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equações de plano] encontrar a equação de um plano
por GHT1810 » Ter Jul 03, 2018 19:42
- 0 Respostas
- 5355 Exibições
- Última mensagem por GHT1810

Ter Jul 03, 2018 19:42
Geometria Analítica
-
- [Equação do Plano Tangente - Plano Paralalelo]
por raimundoocjr » Qui Out 24, 2013 22:10
- 0 Respostas
- 2937 Exibições
- Última mensagem por raimundoocjr

Qui Out 24, 2013 22:10
Cálculo: Limites, Derivadas e Integrais
-
- Equação do plano
por manuoliveira » Qua Mai 23, 2012 17:59
- 1 Respostas
- 1956 Exibições
- Última mensagem por LuizAquino

Qua Mai 23, 2012 20:48
Geometria Analítica
-
- Equação do plano
por Danilo » Qui Out 25, 2012 22:38
- 7 Respostas
- 7100 Exibições
- Última mensagem por MarceloFantini

Qua Out 31, 2012 06:51
Geometria Analítica
-
- [equação do plano]
por lucasdemirand » Dom Set 01, 2013 11:33
- 0 Respostas
- 869 Exibições
- Última mensagem por lucasdemirand

Dom Set 01, 2013 11:33
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
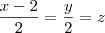 e s: x-2 = y = z, obtenha uma equação geral para o plano determinado por r e s.
e s: x-2 = y = z, obtenha uma equação geral para o plano determinado por r e s. 

 o parâmetro da primeira reta e
o parâmetro da primeira reta e 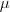 da segunda.
da segunda.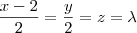
 .
.

 será dada por
será dada por  e a reta
e a reta  por
por 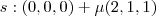 .
. e substitua
e substitua 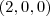 para encontrar o coeficiente que falta.
para encontrar o coeficiente que falta.
