Subespaços Vetoriais

por **felipe_ad** » Sex Ago 27, 2010 19:56

Olá,
Eu até entendi as condições de subespaço vetorial, mas tem exercicios que não consigo resolver. Por isso venho aqui pedir ajuda a quem sabe.
Sao os seguintes:

Verificar se W é subespaço:
(a)V = R4 e W = {( x , y , z , t ) / z = x + 2y e t = x ? 3y}
(b)V = Rn e W = {v ?V / Av = O, A uma matriz m × n e O a matriz nula m × 1}
(c)V = M2× 2 e W = { A / AT = TA, T uma matriz fixada em V }
(d)V = P2 ( x ) e W = { p ( x ) / p ( x ) + p? ( x ) = 0}
(e)V = P2 ( x ) e W = { p ( x ) / grau [ p ( x ) + x2 ] ? 1} ? {o ( x )}, o ( x ) o polinômio nulo.

Agradeço desde já.

por **MarceloFantini** » Sáb Ago 28, 2010 19:31

a)

{ $(x,y,x+2y, x-3y); x,y \in \Re$ }.

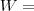
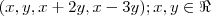
1) O zero pertence pois tomando x e y iguais a zero fica (0,0,0,0).

2) Sejam u = (x_1,y_1,x_1+2y_1, x_1-3y_1)

e

.
$u + v = (x_1,y_1,x_1+2y_1, x_1-3y_1) + (x_2,y_2,x_2+2y_2, x_2-3y_2) = (x_1 + x_2, y_1 + y_2, x_1 + x_2 + 2(y_1 + y_2), x_1 + x_2 -3(y_1 + y_2)) \; \therefore u+v \in W$

3) $\lambda \in \Re ; \; \lambda u = (\lambda x_1, \lambda y_1,\lambda x_1+2\lambda y_1, \lambda x_1-3\lambda y_1) \; \therefore \lambda u \in W$

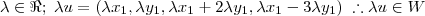
Nos outros basta fazer similar. Você pega a propriedade do subespaço e verifica as condições:

1) Zero tem que estar no subespaço;

2) Dados dois vetores, a soma tem que permanecer no subespaço;

3) Dado uma constante e um vetor, o produto tem que permanecer no subespaço.

Subespaços Vetoriais

Subespaços Vetoriais

Subespaços Vetoriais

Re: Subespaços Vetoriais

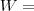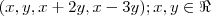Quem está online