Olá,
Eu até entendi as condições de subespaço vetorial, mas tem exercicios que não consigo resolver. Por isso venho aqui pedir ajuda a quem sabe.
Sao os seguintes:
Verificar se W é subespaço:
(a)V = R4 e W = {( x , y , z , t ) / z = x + 2y e t = x ? 3y}
(b)V = Rn e W = {v ?V / Av = O, A uma matriz m × n e O a matriz nula m × 1}
(c)V = M2× 2 e W = { A / AT = TA, T uma matriz fixada em V }
(d)V = P2 ( x ) e W = { p ( x ) / p ( x ) + p? ( x ) = 0}
(e)V = P2 ( x ) e W = { p ( x ) / grau [ p ( x ) + x2 ] ? 1} ? {o ( x )}, o ( x ) o polinômio nulo.
Agradeço desde já.


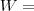 {
{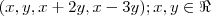 }.
}. e
e  .
.
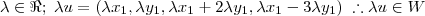


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)