 por Pessoa Estranha » Qui Jan 09, 2014 15:37
por Pessoa Estranha » Qui Jan 09, 2014 15:37
Olá, pessoal! Não estou conseguindo resolver o seguinte exercício:
Obtenha o simétrico do ponto P em relação ao plano:
P=(1,4,2); ?:x-y+z-2=0
Por favor, pode ser só uma dica. Já tentei resolver várias vezes, mas não consigo.
Obrigada!
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por anderson_wallace » Qui Jan 09, 2014 23:56
por anderson_wallace » Qui Jan 09, 2014 23:56
Inicialmente vamos lembrar da definição de equação geral do plano.
Seja

um ponto do plano

e
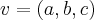
um vetor ortogonal a

, a equação geral do plano

é definida como
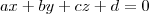
, onde

Então note que com a equação geral vc tem um vetor ortogonal ao plano, que nesse caso é
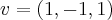
Agora podemos encontrar uma reta ortogonal a

que passa pelo ponto

, e como o ponto simétrico a P está contido nessa reta, ele pode ser escrito como
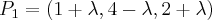
(Verifique!).
Perceba que basta vc encontrar o valor para

tal que a distância do ponto P ao plano

seja igual a distância do ponto P1 ao plano

.
-
anderson_wallace
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Seg Dez 30, 2013 17:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ciência e Tecnologia
- Andamento: cursando
 por Pessoa Estranha » Sex Jan 10, 2014 16:08
por Pessoa Estranha » Sex Jan 10, 2014 16:08
Olá! Obrigada por responder!
Bem, pensei assim também, mas fiquei na dúvida, pois como podemos garantir que o ponto P está na reta ortogonal ao plano? (não sei se estou dizendo um absurdo, mas podemos imaginar um plano "atravessado" por uma reta ortogonal e que não passa por P, não é?).
Desculpe, estou precisando estudar mais este conteúdo, mas foi o que pensei....
Obrigada!
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por anderson_wallace » Sex Jan 10, 2014 16:45
por anderson_wallace » Sex Jan 10, 2014 16:45
Seu raciocínio faz todo sentido, afinal existem infinitas retas ortogonais ao plano

. Mas note o modo como essa reta em particular foi obtida. Inicialmente tomamos um vetor ortogonal ao plano que foi dado pela própria equação geral do plano
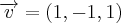
, daí encontramos a reta ortogonal a

que tem como vetor diretor o vetor
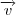
, e que
passa pelo ponto P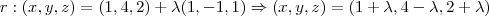
Ou seja, na própria obtenção da reta definimos que ela passa pelo ponto P.
-
anderson_wallace
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Seg Dez 30, 2013 17:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ciência e Tecnologia
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria Analitica] Urgente!
por mih123 » Qua Mar 27, 2013 10:16
- 1 Respostas
- 1476 Exibições
- Última mensagem por timoteo

Qua Mar 27, 2013 18:03
Geometria Analítica
-
- [Geometria Analítica] Retas perpendiculares - Urgente!
por Pessoa Estranha » Qua Jan 08, 2014 18:16
- 5 Respostas
- 2777 Exibições
- Última mensagem por Pessoa Estranha

Qui Jan 09, 2014 09:37
Geometria Analítica
-
- exercicio geometria analitica
por llucasws » Seg Ago 16, 2010 17:31
- 1 Respostas
- 5239 Exibições
- Última mensagem por alexandre32100

Ter Ago 17, 2010 01:05
Geometria Analítica
-
- Exercício Geometria Analítica
 por GuiFerronato » Qua Nov 19, 2014 17:28
por GuiFerronato » Qua Nov 19, 2014 17:28
- 1 Respostas
- 1553 Exibições
- Última mensagem por adauto martins

Qui Nov 20, 2014 10:46
Geometria Analítica
-
- [geometria analitica] EXERCÍCIO DE VETOR
por luiz_henriquear » Ter Out 25, 2011 20:07
- 1 Respostas
- 2268 Exibições
- Última mensagem por MarceloFantini

Qua Out 26, 2011 15:14
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 um ponto do plano
um ponto do plano  e
e 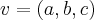 um vetor ortogonal a
um vetor ortogonal a  , a equação geral do plano
, a equação geral do plano  é definida como
é definida como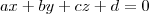 , onde
, onde 
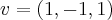
 que passa pelo ponto
que passa pelo ponto  , e como o ponto simétrico a P está contido nessa reta, ele pode ser escrito como
, e como o ponto simétrico a P está contido nessa reta, ele pode ser escrito como 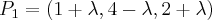 (Verifique!).
(Verifique!). tal que a distância do ponto P ao plano
tal que a distância do ponto P ao plano  seja igual a distância do ponto P1 ao plano
seja igual a distância do ponto P1 ao plano  .
.

 . Mas note o modo como essa reta em particular foi obtida. Inicialmente tomamos um vetor ortogonal ao plano que foi dado pela própria equação geral do plano
. Mas note o modo como essa reta em particular foi obtida. Inicialmente tomamos um vetor ortogonal ao plano que foi dado pela própria equação geral do plano 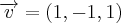 , daí encontramos a reta ortogonal a
, daí encontramos a reta ortogonal a  que tem como vetor diretor o vetor
que tem como vetor diretor o vetor 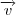 , e que passa pelo ponto P
, e que passa pelo ponto P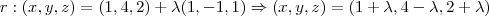




![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.