 por luankaique » Qui Jul 25, 2013 22:34
por luankaique » Qui Jul 25, 2013 22:34
Fala pessoal
Estou com dúvida em uma questão. A resposta é P(1,0,0), consegui até entender o raciocínio mas queria saber como fazer a questão "na tora", desenvolvendo tudo certinho.
Sejam:
A(1,1,1)
B(0,0,1)
r: X = (1,0,0) + t(1,1,1)
Determine os pontos de r equidistantes de A e B:
-
luankaique
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Jul 25, 2013 22:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Industrial Mecânica
- Andamento: cursando
 por MateusL » Qui Jul 25, 2013 23:06
por MateusL » Qui Jul 25, 2013 23:06
A distância de um ponto
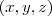
até o ponto

é:

E até o ponto

:

Os pontos equidistantes de

e

são os pontos
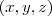
que satisfazem:


Simplificando, chegamos a:

Além disso, temos que:
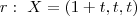
Então, para os pontos pertencentes a

, teremos

e

.
Temos, então, o seguinte sistema:
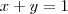


Resolvendo, encontramos

, portanto, o ponto procurado é

.
Abraço!
-
MateusL
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Qua Jul 17, 2013 23:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por luankaique » Sex Jul 26, 2013 14:11
por luankaique » Sex Jul 26, 2013 14:11
Consegui entender a questão.
Muito obrigado!
-
luankaique
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Jul 25, 2013 22:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Industrial Mecânica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Retas e pontos
por Neydimara » Ter Ago 05, 2014 19:21
- 1 Respostas
- 1063 Exibições
- Última mensagem por Cleyson007

Qua Ago 06, 2014 21:14
Geometria Analítica
-
- Retas e pontos
por Neydimara » Ter Ago 05, 2014 19:27
- 3 Respostas
- 1601 Exibições
- Última mensagem por jcmatematica

Sáb Set 27, 2014 15:24
Geometria Analítica
-
- Relação entre cordas entre dois pontos de retas.
por janderson77 » Seg Dez 02, 2013 12:00
- 0 Respostas
- 2059 Exibições
- Última mensagem por janderson77

Seg Dez 02, 2013 12:00
Trigonometria
-
- [RETAS] Descobrir ponto através de retas
 por renan_a » Qui Set 27, 2012 11:10
por renan_a » Qui Set 27, 2012 11:10
- 5 Respostas
- 3094 Exibições
- Última mensagem por renan_a

Sáb Set 29, 2012 18:37
Geometria Analítica
-
- [Pontos críticos - Derivadas] Ajuda com pontos críticos
por jonaskessinger » Qui Dez 13, 2012 18:16
- 1 Respostas
- 3585 Exibições
- Última mensagem por Russman

Qui Dez 13, 2012 19:35
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


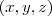 até o ponto
até o ponto  é:
é:
 :
:



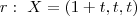
 , teremos
, teremos  e
e  .
.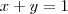
 , portanto, o ponto procurado é
, portanto, o ponto procurado é  .
.
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
